电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017:修订间差异
无编辑摘要 标签:移动版编辑 移动版网页编辑 |
无编辑摘要 标签:移动版编辑 移动版网页编辑 |
||
| (未显示同一用户的1个中间版本) | |||
| 第54行: | 第54行: | ||
式(1)中的相关参数见式(2)。 | 式(1)中的相关参数见式(2)。 | ||
\begin{aligned} | <math>\begin{aligned} | ||
& c_{k}=\mid b_{k}+ja_{k}\mid=\sqrt{a_{k}^{2}+b_{k}^{2}} \\ | & c_{k}=\mid b_{k}+ja_{k}\mid=\sqrt{a_{k}^{2}+b_{k}^{2}} \\ | ||
& Y_{\mathrm{ | & Y_{\mathrm{c},k}=\frac{c_{k}}{\sqrt{2}} | ||
\end{aligned}</math> | |||
\end{aligned} | |||
<math>\varphi_k=\pi+\arctan\left(\frac{a_k}{b_k}\right),\text{若 }b_k<0\quad\varphi_k=\arctan\left(\frac{a_k}{b_k}\right),\text{若 }b_k>0\varphi_k=\frac{\pi}{2}\text{,若 }b_k=0\text{ 且 }a_k>0\quad\varphi_k=-\frac{\pi}{2}\text{,若 }b_k=0\text{ 且 }a_k<0</math> | |||
………(2) | ………(2) | ||
| 第480行: | 第475行: | ||
仪器的输出“输出1”(见图1)应能分别给出电流或电压在DFT 后的每一个系数 a<sub>k</sub> 和b<sub>k</sub>, 以及 Y<sub>c,k</sub>,即计算出的每一个频率分量的值。 | 仪器的输出“输出1”(见图1)应能分别给出电流或电压在DFT 后的每一个系数 a<sub>k</sub> 和b<sub>k</sub>, 以及 Y<sub>c,k</sub>,即计算出的每一个频率分量的值。 | ||
[[文件:电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017_图1 测量仪器的通用架构.jpeg]] | [[文件:电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017_图1 测量仪器的通用架构.jpeg|400px]] | ||
图 1 测量仪器的通用架构 | 图 1 测量仪器的通用架构 | ||
| 第599行: | 第594行: | ||
图 2 和 图 3 给 出 了 测 量 布 置 。 | 图 2 和 图 3 给 出 了 测 量 布 置 。 | ||
[[文件:电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017_图2 用于单相设备发射测量的测量布置.jpeg]] | [[文件:电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017_图2 用于单相设备发射测量的测量布置.jpeg|400px]] | ||
说明: | 说明: | ||
| 第617行: | 第612行: | ||
图 2 用 于 单 相 设 备 发 射 测 量 的 测 量 布 置 | 图 2 用 于 单 相 设 备 发 射 测 量 的 测 量 布 置 | ||
[[文件:电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017_图3 用于三相设备发射测量的测量布置.jpeg]] | [[文件:电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017_图3 用于三相设备发射测量的测量布置.jpeg|400px]] | ||
说明: | 说明: | ||
| 第653行: | 第648行: | ||
b) 对于三相电源供电情况,三个线电压应具有0°、120°±1.5°、240°±1.5°的相位关系。 | b) 对于三相电源供电情况,三个线电压应具有0°、120°±1.5°、240°±1.5°的相位关系。 | ||
c) 在 EUT 连接并运行在特定试验条件下时,EUT 的试验电压U | c) 在 EUT 连接并运行在特定试验条件下时,EUT 的试验电压U 的电压谐波畸变不应超过以下数值: | ||
——3次谐波,0.9%; | ——3次谐波,0.9%; | ||
| 第682行: | 第675行: | ||
b) 输出电压应维持在标称值的±2%,频率应维持在标称值的±0.5%范围之内。 | b) 输出电压应维持在标称值的±2%,频率应维持在标称值的±0.5%范围之内。 | ||
c) 对于三相电源供电情况,电压不平衡度应低于IEC 61000-2-2 中所规定的不平衡电压兼容水 平的50%。 | c) 对于三相电源供电情况,电压不平衡度应低于IEC 61000-2-2 中所规定的不平衡电压兼容水 平的50%。 | ||
| 第691行: | 第682行: | ||
——5次谐波,1.5%; | ——5次谐波,1.5%; | ||
——3次与7次谐波,1.25%; | |||
——11次谐波,0.7%; | ——11次谐波,0.7%; | ||
| 第719行: | 第710行: | ||
5.5.1 分群和平滑 | 5.5.1 分群和平滑 | ||
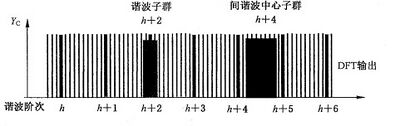
为评估谐波,DFT 的输出“输出1”(见图1)首先根据式(8)进行分群,分群为两个邻近谐波之间的 各中间分量的平方和,如图4所示。仅使用2次谐波以上的中间分量。得到的第h 次谐波群(对应涂黑 区域的中心分量) | 为评估谐波,DFT 的输出“输出1”(见图1)首先根据式(8)进行分群,分群为两个邻近谐波之间的 各中间分量的平方和,如图4所示。仅使用2次谐波以上的中间分量。得到的第h 次谐波群(对应涂黑 区域的中心分量)具有幅值Y<sub>g,h</sub> (对于50 Hz 系统,该幅值等于整数倍谐波频谱分量的平方、紧邻的k= N×h-4 到 k=N×h+ 4 范围内各频谱分量平方与k=N×h-5 和 k=N×h+ 5 频谱分量平方一半 的和的平方根)。 | ||
<math>Y_{g,h}^2=\frac{1}{2}\cdot Y_{C,(N\times h)-N/2}^2+\sum_{k=(-N/2)+1}^{(N/2)-1}Y_{C,(N\times h)+k}^2+\frac{1}{2}\cdot Y_{C,(N\times h)+N/2}^2</math>…………(8) | |||
注:式中仅对2次谐波以上的中间分量进行计算。 | 注:式中仅对2次谐波以上的中间分量进行计算。 | ||
| 第727行: | 第718行: | ||
式中: | 式中: | ||
Y<sub>c,(NXh)+k</sub> —— 与 DFT 输出值(频谱分量)对应的方均根值; | |||
(N×h)+k—— 频谱分量的次数; | |||
( | |||
Y<sub>g,h</sub> —— 谐波群方均根值。 | |||
[[文件:电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017_图4谐波群和间谐波群示意图(图示为50Hz电源).jpeg|400px]] | |||
图 4 谐波群和间谐波群示意图(图示为50 Hz 电源) | 图 4 谐波群和间谐波群示意图(图示为50 Hz 电源) | ||
注:图4中所示的间谐波群仅为明晰定义(间谐波电流评估参见附录 A)。 | 注:图4中所示的间谐波群仅为明晰定义(间谐波电流评估参见附录 A)。 | ||
应对根据式(8)(图1中的“输出2a”) | 应对根据式(8)(图1中的“输出2a”)输出的各次谐波的方均根值Y<sub>g,h</sub> 进行信号的平滑处理。使用 一阶低通数字滤波器,其时间常数为1.5 s, 如图5所示。 | ||
[[文件:电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017_图5 数字低通滤波器的实现原理[z一'表示时间窗延迟,a、β为滤波器系数(数值见表 2)].jpeg]] | [[文件:电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017_图5 数字低通滤波器的实现原理[z一'表示时间窗延迟,a、β为滤波器系数(数值见表 2)].jpeg|400px]] | ||
| 第784行: | 第760行: | ||
|} | |} | ||
对于基波分量Y<sub>H,1</sub>, 应对从“输出1”输出的方均根值YH,1 进行同样的平滑处理(若需要,例如对于 IEC61000-3-2 的 C 类以及可能的畸变系数)。 | |||
如果根据3.3, | 如果根据3.3,发射限值包含了通过谐波分量Y<sub>H,A</sub> 导出的畸变因数THD<sub>y</sub> 或PWHD<sub>H,Y</sub>, 则应通过 “输出1”的值来计算。 | ||
如果根据3.3,发射限值包含了根据谐波分量 | 如果根据3.3,发射限值包含了根据谐波分量 Y<sub>g,h</sub> 或 Y<sub>sg,h</sub>, 导出的畸变率 THDG<sub>y</sub> 、THDS<sub>Y</sub>、 PWHD<sub>g,Y</sub> 或PWHD<sub>sg,Y</sub>, 则通过“输出2a” 的值来计算。 | ||
如果在相关标准中需要对上述畸变率进行平滑处理,应使用一阶低通数字滤波器,其时间常数为1.5 s,如图5所示,滤波器的相关系数见表2。 | |||
对有功功率P 和功率因数(若需要,例如IEC 61000-3-2对 C 类和D 类的要求),应对有功功率和功 率因数的模数进行相似的平滑处理 。 | 对有功功率P 和功率因数(若需要,例如IEC 61000-3-2对 C 类和D 类的要求),应对有功功率和功 率因数的模数进行相似的平滑处理 。 | ||
| 第798行: | 第772行: | ||
注:如果用来测量功率P 的时间分辨率约为200 ms, 则可使用外部功率表。因此可以预先在平滑模块前增加外部 功率表的输入,见图1。 | 注:如果用来测量功率P 的时间分辨率约为200 ms, 则可使用外部功率表。因此可以预先在平滑模块前增加外部 功率表的输入,见图1。 | ||
为与谐波电压的调查相协调(见 IEC 61000-4-30),极力推荐一种更好的平滑方式:在根据式(8)计 算出的各谐波分量均方根值的基础上,其输出是对连续15个时间窗结果的平滑,每个时间窗( | 为与谐波电压的调查相协调(见 IEC 61000-4-30),极力推荐一种更好的平滑方式:在根据式(8)计 算出的各谐波分量均方根值的基础上,其输出是对连续15个时间窗结果的平滑,每个时间窗(大约200 ms)或每15个时间窗(大约3 s)更新 一 次。 | ||
5.5.2 发射限值的符合性 | 5.5.2 发射限值的符合性 | ||
应依照相关标准(例如 IEC 61000-3-2 、IEC 61000-3-6 、IEC61000-3-12 和 IEC 61000-4-30) | 应依照相关标准(例如 IEC 61000-3-2 、IEC 61000-3-6 、IEC61000-3-12 和 IEC 61000-4-30)中给定的条件,在进行数据的统计处理后再行评估发射是否符合限值。 | ||
=== 5.6 电压谐波子群的评估 === | === 5.6 电压谐波子群的评估 === | ||
| 第814行: | 第782行: | ||
傅立叶变换分析假设信号是稳态的。然而,供电系统的电压幅值可能会出现波动,将谐波分量的能 量扩散到与之邻近频率的频谱上。为提高电压评估准确度,DFT 后每5 Hz 频率分量的输出 Uc,k, 应 根据图6和式(9)加以分群: | 傅立叶变换分析假设信号是稳态的。然而,供电系统的电压幅值可能会出现波动,将谐波分量的能 量扩散到与之邻近频率的频谱上。为提高电压评估准确度,DFT 后每5 Hz 频率分量的输出 Uc,k, 应 根据图6和式(9)加以分群: | ||
…………………………(9) | <math>Y_{sg,h}^{2}=\sum_{k=-1}^{1}Y_{\mathrm{C},(N\times h)+k}^{2}</math>…………………………(9) | ||
式中, | 式中, | ||
Y<sub>c,(NXh)+k</sub> —— 与 DFT 输出值(频谱分量)对应的方均根值; | |||
(N×h)+k—— 频谱分量的次数; | (N×h)+k—— 频谱分量的次数; | ||
Y<sub>sg,h</sub> ——谐波子群的方均根值。 | |||
用符号I替代Y 则表示电流,单位为安培(A); 符 号U 代 替Y 则表示电压,单位为伏特(V)。 | |||
[[文件:电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017_图6 谐波子群和间谐波中心子群示例(图示为50Hz电源).jpeg|400px]] | |||
图 6 谐波子群和间谐波中心子群示例(图示为50 Hz 电 源 ) | 图 6 谐波子群和间谐波中心子群示例(图示为50 Hz 电 源 ) | ||
| 第873行: | 第840行: | ||
附 录 A | == 附 录 A == | ||
(资料性附录) 间谐波的测量 | (资料性附录) 间谐波的测量 | ||
| 第887行: | 第854行: | ||
——音频放大器的噪声; | ——音频放大器的噪声; | ||
——电动机和发电机的附加转矩; | |||
——骚扰过零点检测,例如在调光器中; | ——骚扰过零点检测,例如在调光器中; | ||
| 第899行: | 第866行: | ||
与间谐波分量有关的频谱分量不仅有幅值的变化,而且还有频率的变化。在两个连续的谐波分量 之间有一组频谱分量,从而构成一个间谐波群。这种组合给出了在两个离散的谐波分量之间所有间谐 波分量的综合值,也包含了谐波分量波动的影响。根据供电频率,可用式(A.1) 计算间谐波群的值: | 与间谐波分量有关的频谱分量不仅有幅值的变化,而且还有频率的变化。在两个连续的谐波分量 之间有一组频谱分量,从而构成一个间谐波群。这种组合给出了在两个离散的谐波分量之间所有间谐 波分量的综合值,也包含了谐波分量波动的影响。根据供电频率,可用式(A.1) 计算间谐波群的值: | ||
…………………………(A.1) | <math>Y_{i_{g},h}^{2}=\sum_{k=1}^{N-1}Y_{C,(N\times h)+k}^{2}</math>…………………………(A.1) | ||
注:式中下标ig,h 表示第h 次间谐波群(见图4和3.4.3)。本部分旨在将介于第h 次和第h+1 次谐波之间的间谐 | 注:式中下标ig,h 表示第h 次间谐波群(见图4和3.4.3)。本部分旨在将介于第h 次和第h+1 次谐波之间的间谐 波群的方均根值用Y<sub>ig,h</sub> 来表示。例如,5次谐波和6次谐波之间的间谐波群表示为Y<sub>g,5</sub>。 | ||
从式(A.1) 中剔除紧邻谐波频率的分量,部分地减少了谐波幅值和相位角波动的影响。同样,为了 确定间谐波中心子群的方均根值Yg,h, 其分量,即图1中DFT 的“输出1”的输出数据,用式(A.2) 重新 组合(见3.4.4): | 从式(A.1) 中剔除紧邻谐波频率的分量,部分地减少了谐波幅值和相位角波动的影响。同样,为了 确定间谐波中心子群的方均根值Yg,h, 其分量,即图1中DFT 的“输出1”的输出数据,用式(A.2) 重新 组合(见3.4.4): | ||
<math>Y_{isg,h}^{2}=\sum_{k=2}^{N-2}Y_{C,(N\times h)+k}^{2}</math>………………………(A.2) | |||
该式中,Y<sub>c,(NXk)+k</sub> 是 由DFT 得到的频率超出第h 次谐波频率的相应频谱分量的方均根值,而 Y<sub>isg,h</sub> 则是第h 次间谐波中心子群的方均根值,例如,5次谐波和6次之间的间谐波中心子群表示为 Y<sub>isg,5</sub>,见图6和3.4.4。 | |||
注1:因为非稳态谐波会在谐波旁边生成旁带,与所考虑谐波直接相邻的频谱分量(k=1 和9或11)可能表征其幅 值和相位角的变化。所以,为给出间谐波中心子群,要把它们从间谐波群中剔除,参见图6。 | 注1:因为非稳态谐波会在谐波旁边生成旁带,与所考虑谐波直接相邻的频谱分量(k=1 和9或11)可能表征其幅 值和相位角的变化。所以,为给出间谐波中心子群,要把它们从间谐波群中剔除,参见图6。 | ||
| 第927行: | 第888行: | ||
附 录 B | == 附 录 B == | ||
(资料性附录) | (资料性附录) | ||
| 第933行: | 第894行: | ||
谐波频率范围以上至9 kHz 的测量 | 谐波频率范围以上至9 kHz 的测量 | ||
B.1 概述 | === B.1 概述 === | ||
信号(电流或电压)中高于40次谐波频率(约2 kHz) 且又低于低频范围上限(9 kHz) 的分量是由于 诸如此类的现象而产生的: | 信号(电流或电压)中高于40次谐波频率(约2 kHz) 且又低于低频范围上限(9 kHz) 的分量是由于 诸如此类的现象而产生的: | ||
| 第955行: | 第916行: | ||
另外,如测量仪器内部有滤波器组合和足够大的动态测量范围,即使不使用上述滤波器也可分析 2 kHz~9 kHz频率范围内的信号。 | 另外,如测量仪器内部有滤波器组合和足够大的动态测量范围,即使不使用上述滤波器也可分析 2 kHz~9 kHz频率范围内的信号。 | ||
B.2 基本仪器 | === B.2 基本仪器 === | ||
这种较高频率范围的测量,可按4.4.1进行离散傅立叶变换,且按照本附录进行改造。 | 这种较高频率范围的测量,可按4.4.1进行离散傅立叶变换,且按照本附录进行改造。 | ||
| 第963行: | 第924行: | ||
由于要测量的信号较弱,可用带通滤波器抑制基波和9 kHz 频率以上的分量幅值,从而大大减少 测量的不确定度。对基波频率的衰减要超过560倍(55 dB)。 | 由于要测量的信号较弱,可用带通滤波器抑制基波和9 kHz 频率以上的分量幅值,从而大大减少 测量的不确定度。对基波频率的衰减要超过560倍(55 dB)。 | ||
注1:与基波电流、电压的幅值相比,待测分量幅值在2×10-⁵~5×10- | 注1:与基波电流、电压的幅值相比,待测分量幅值在2×10-⁵~5×10<sup>-2</sup>范围内。 | ||
采样频率应按已有的信号分析的既定规定选取,使频率高达9 kHz 的分量都能测到。可采用宽度 为200 ms 的矩形数据采集窗,约相当于50 Hz(60 Hz)系统的10(12)个周期。这样,两个连续的被测分 量 | 采样频率应按已有的信号分析的既定规定选取,使频率高达9 kHz 的分量都能测到。可采用宽度 为200 ms 的矩形数据采集窗,约相当于50 Hz(60 Hz)系统的10(12)个周期。这样,两个连续的被测分 量 Y<sub>c,f</sub>之间的频率差是5 Hz。 | ||
注2:采样频率无需与电源频率同步。 | 注2:采样频率无需与电源频率同步。 | ||
频率为f | 频率为f 的分量的方均根值为Y<sub>c,f</sub>, 例如Y<sub>c,3 160</sub>是频率3160 Hz 分量的方均根值。 | ||
电流与电压输入电路应分别满足5.1与5.2的要求。 | 电流与电压输入电路应分别满足5.1与5.2的要求。 | ||
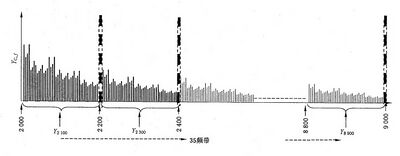
B.3 分群 | === B.3 分群 === | ||
DFT 的原始输出(图1中的“输出1”)应按200 Hz 的带宽分群(见图 B.1), | DFT 的原始输出(图1中的“输出1”)应按200 Hz 的带宽分群(见图 B.1), 起点在高于谐波范围之上的第1个中心带宽。第1个群的中心频率对于50 Hz 以及60 Hz 系统分别为2.1kHz 和2.5 kHz。 每个频带的输出YB,b是方均根值,见式(B.1): | ||
<math>Y_{B,b}=\sqrt{\sum_{f=b-95\mathrm{Hz}}^{b+100\mathrm{Hz}}Y_{\mathrm{C},f}^{2}}</math>…………………………(B.1) | |||
式中: | 式中: | ||
Y<sub>B,b</sub>——每个频带的输出的方均根值; | |||
Y<sub>c,f</sub>——频率为f 的分量的方均根值。 | |||
用符号 I 替代Y 则表示电流,单位为安培(A); 符号U 代替Y 则表示电压,单位为伏特(V) | |||
注1:选取200 Hz频带分群是为了与CISPR 16-1-2中对9kHz以上的信号带宽处理相一致。 | |||
注2:中心频率b 如2100 Hz 、2300 Hz 、2500 Hz等频率代表了该段频带。最高的中心频率为8900 Hz,见图B.1。 | 注2:中心频率b 如2100 Hz 、2300 Hz 、2500 Hz等频率代表了该段频带。最高的中心频率为8900 Hz,见图B.1。 | ||
| 第995行: | 第954行: | ||
注3:对于60 Hz电力系统,谐波范围以上的分量频率大于2400 Hz。 | 注3:对于60 Hz电力系统,谐波范围以上的分量频率大于2400 Hz。 | ||
注4:当谐波范围以50次谐波结尾时,式(B.1)对于6>2500的50Hz电力系统以及6>3100的60Hz电力系统均适用。 | |||
[[文件:电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017_图B.1 50Hz电力系统中40次谐波频率以上至9kHz的频带范围内测量示意图.jpeg]] | [[文件:电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017_图B.1 50Hz电力系统中40次谐波频率以上至9kHz的频带范围内测量示意图.jpeg|400px]] | ||
图 B.1 50Hz电力系统中40次谐波频率以上至9 kHz 的频带范围内测量示意图 | 图 B.1 50Hz电力系统中40次谐波频率以上至9 kHz 的频带范围内测量示意图 | ||
B.4 发射评估用的测量布置 | === B.4 发射评估用的测量布置 === | ||
为了提高发射评估测量结果的可重复性,需要明确定义电源侧的阻抗。因此应在电源端以及 EUT 端之间插入人工电源网络(AMN), 以使电源侧在2 kHz~9kHz 范围内的阻抗特性标准化,测量布置 见图 B.2。 | 为了提高发射评估测量结果的可重复性,需要明确定义电源侧的阻抗。因此应在电源端以及 EUT 端之间插入人工电源网络(AMN), 以使电源侧在2 kHz~9kHz 范围内的阻抗特性标准化,测量布置 见图 B.2。 | ||
| 第1,011行: | 第971行: | ||
发射测量时,需要测量 AMN 与 EUT 之间导线上的电流,如图 B.3 中的B 点。 | 发射测量时,需要测量 AMN 与 EUT 之间导线上的电流,如图 B.3 中的B 点。 | ||
[[文件:电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017_图B.2 通用的测量布置.jpeg|400px]] | |||
[[文件:电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017_图B.2 通用的测量布置.jpeg]] | |||
图 B.2 通 用 的 测 量 布 置 | 图 B.2 通 用 的 测 量 布 置 | ||
| 第1,019行: | 第977行: | ||
网络2是由3个网络1单元组成,并将所有的中性点连接在一起。 | 网络2是由3个网络1单元组成,并将所有的中性点连接在一起。 | ||
[[文件:电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017_图B.3 适用于16A电流及以下测量的人工电源网络.jpeg|400px]] | |||
[[文件:电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017_图B.3 适用于16A电流及以下测量的人工电源网络.jpeg]] | |||
图 B.3 适用于16 A 电流及以下测量的人工电源网络 | 图 B.3 适用于16 A 电流及以下测量的人工电源网络 | ||
注:如果使用交流电源,其电感与电阻分别不可超过160 μH 和0 . 1Ω。 | 注:如果使用交流电源,其电感与电阻分别不可超过160 μH 和0.1Ω。 | ||
B.5 性能要求 | === B.5 性能要求 === | ||
用单频率信号进行测量时,总体测量不确定度(测试仪器包括分流器或 CT) 不得超过被测电流的 ±10%。仪器制造商应明确说明该±10%的不确定度所适用的测量范围。 | 用单频率信号进行测量时,总体测量不确定度(测试仪器包括分流器或 CT) 不得超过被测电流的 ±10%。仪器制造商应明确说明该±10%的不确定度所适用的测量范围。 | ||
| 第1,041行: | 第997行: | ||
当 A 直接连至 N 时,在 B 和 N 之间测量,AMN 应提供给 EUT 的阻抗特性,应在图 B.4 所示 2 kHz~9 kHz特性的±5%范围内。因此需要选择元件的容差,以使得在 EUT 电流、温度、频率在运 行条件之内时,阻抗特性不超过其容差范围。记住要根据该容差设计AMN 的物理布局、封装以及温度控制措施。 | 当 A 直接连至 N 时,在 B 和 N 之间测量,AMN 应提供给 EUT 的阻抗特性,应在图 B.4 所示 2 kHz~9 kHz特性的±5%范围内。因此需要选择元件的容差,以使得在 EUT 电流、温度、频率在运 行条件之内时,阻抗特性不超过其容差范围。记住要根据该容差设计AMN 的物理布局、封装以及温度控制措施。 | ||
[[文件:电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017_图B.4从EUT侧看人工电源网络阻抗.jpeg|400px]] | |||
[[文件:电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017_图B.4从EUT侧看人工电源网络阻抗.jpeg]] | |||
图 B.4 从 EUT 侧 看 人 工 电 源 网 络 阻 抗 | 图 B.4 从 EUT 侧 看 人 工 电 源 网 络 阻 抗 | ||
| 第1,049行: | 第1,003行: | ||
在2050 Hz 以及2450 Hz, 输出阻抗分别为3.745051以及3.868689Ω。频率f 大于3kHz 时的 输出阻抗由式(B.2) 计算: | 在2050 Hz 以及2450 Hz, 输出阻抗分别为3.745051以及3.868689Ω。频率f 大于3kHz 时的 输出阻抗由式(B.2) 计算: | ||
<math>\mid z\mid=\sqrt{8.819+1.23\times10^{-7}\times f^2\ln(f)}</math> …………………………(B.2) | |||
式 中 : | 式 中 : | ||
| 第1,059行: | 第1,013行: | ||
附 录 C | == 附 录 C == | ||
(资料性附录) | (资料性附录) | ||
| 第1,069行: | 第1,023行: | ||
注:在本部分中,除非另有说明,电压、电流的值均用方均根值表示。 | 注:在本部分中,除非另有说明,电压、电流的值均用方均根值表示。 | ||
C.1 时域信号表征和频域信号表征的功率等值 | === C.1 时域信号表征和频域信号表征的功率等值 === | ||
帕斯瓦尔(Parseval) 关系式,也称为瑞利(Rayleigh) 能量定理,定义信号功率(或能量)在时域和频 域中的等价关系,见式(C.1): | 帕斯瓦尔(Parseval) 关系式,也称为瑞利(Rayleigh) 能量定理,定义信号功率(或能量)在时域和频 域中的等价关系,见式(C.1): | ||
…………………………(C.1) | <math>\int_{-\infty}^{+\infty}\left[g\left(t\right)\right]^{2}\mathrm{d}t=\frac{1}{2\pi}\int_{-\infty}^{+\infty}\left|G\left(\mathrm{j}\omega\right)\right|^{2}\mathrm{d}\omega</math>…………………………(C.1) | ||
式中: | 式中: | ||
| 第1,083行: | 第1,037行: | ||
注:由于功率与电压或电流的平方成正比,因此,信号的平方被看作信号的“功率”。例如,如果设g(t)是某电压的 时域函数,则公式左侧(时域)的物理量纲应该是 V²s (能量)。傅立叶变换表示的是电压的频谱密度,在上例 中,G(jw)的量纲就是 V/Hz 或者Vs, 即该公式右侧的量纲也是 V²s(能量)。 | 注:由于功率与电压或电流的平方成正比,因此,信号的平方被看作信号的“功率”。例如,如果设g(t)是某电压的 时域函数,则公式左侧(时域)的物理量纲应该是 V²s (能量)。傅立叶变换表示的是电压的频谱密度,在上例 中,G(jw)的量纲就是 V/Hz 或者Vs, 即该公式右侧的量纲也是 V²s(能量)。 | ||
如果为非周期函数,则其频谱是连续的。但是,如果是周期函数,则它可以用在时间窗 T 内表征, 即用该时间窗的无限重复可生成整个函数g(t) 。 该时间受限信号的傅立叶变换就不再连续,而是由按 | 如果为非周期函数,则其频谱是连续的。但是,如果是周期函数,则它可以用在时间窗 T 内表征, 即用该时间窗的无限重复可生成整个函数g(t) 。 该时间受限信号的傅立叶变换就不再连续,而是由按 f<sub>w</sub>=1/T 频率分隔的频谱分量构成。时间窗 T 和在频率f=k×f<sub>w</sub> 的频谱分量(复数)方均根值平方G 的积,近似表示从f-f<sub>w</sub>/2 到 f+f<sub>w</sub>/2 积分的连续频谱密度的“能量”。由所有频谱分量贡献的 “能量”总和就等值于在时间窗内该时域函数的“能量”。将该“能量”除以时间窗的时间 T。就 得 到 式(C.2): | ||
…………………………(C.2) | <math>\frac{1}{T_{w}}\int_{-T_{w}/2}^{+T_{w}/2}\left[g\left(t\right)\right]^{2}\mathrm{d}t=\sum_{k--\infty}^{\infty}\left|G_{k}\right|^{2}</math>…………………………(C.2) | ||
式中,左边相当于时间函数在时间窗内的平均“功率”,右边对应于频域内所有频谱分量的总“功 率”。 | 式中,左边相当于时间函数在时间窗内的平均“功率”,右边对应于频域内所有频谱分量的总“功 率”。 | ||
| 第1,093行: | 第1,045行: | ||
傅立叶变换的一个性质,是在负数频率的频谱分量是在同一正数频率频谱分量的共轭复数,即“功 率”频谱关于频率f=0 是对称的。将频谱的负数部分取正,与正数部分叠加,则式(C.2) 可简化为 式(C.3): | 傅立叶变换的一个性质,是在负数频率的频谱分量是在同一正数频率频谱分量的共轭复数,即“功 率”频谱关于频率f=0 是对称的。将频谱的负数部分取正,与正数部分叠加,则式(C.2) 可简化为 式(C.3): | ||
<math>\frac{1}{T_{w}}\int_{-T_{w}/2}^{+T_{w}/2}\left[g\left(t\right)\right]^{2}\mathrm{d}t=G_{0}^{2}+2\sum_{k=1}^{\infty}\mid G_{k}\mid^{2}</math>…………………………(C.3) | |||
按照本部分中式(3)的傅立叶分量的幅值c<sub>k</sub>, 其定义与 T<sub>w</sub>/2 而 不 是 T<sub>w</sub>有 关(c。除外,与 T<sub>w</sub> 有 关),即c<sub>k</sub>=2×G 或 C<sub>k</sub>=√2×G<sub>k</sub> 。 因此,式(C.3) 可改写成式(C.4): | |||
<math>\frac{1}{T_{w}}\int_{-T_{w}/2}^{+T_{w}/2}\left[g\left(t\right)\right]^{2}\mathrm{d}t=c_{0}^{2}+\sum_{k=1}^{\infty}\mid C_{k}\mid^{2}=\sum_{k=0}^{\infty}\mid C_{k}\mid^{2}</math>………………(C.4) | |||
………………(C.4) | |||
实际上,求和式中系数的个数应限制:k=1,…K 。 | 实际上,求和式中系数的个数应限制:k=1,…K 。 如果对于频率f<sub>k</sub>≤K×f<sub>w</sub> 有限带宽信号,下标k>K 的系数则没有“功率”,在式(C.4) 的求和式里可不考虑这些系数。但该频率fk 应远超过仪器的 工作频率范围 。 | ||
=== C.2 数字化实现的特性 === | |||
C.2 数字化实现的特性 | |||
本部分考虑了数字仪表。为了满足香农定理,应该以f,>2×f 的采样频率对时域信号进行采样, 所以,原则上可以计算出一直到C 的所有系数。一个时间窗内的采样点数为N=f,×Tm。 | 本部分考虑了数字仪表。为了满足香农定理,应该以f,>2×f 的采样频率对时域信号进行采样, 所以,原则上可以计算出一直到C 的所有系数。一个时间窗内的采样点数为N=f,×Tm。 | ||
| 第1,115行: | 第1,063行: | ||
式 中 : | 式 中 : | ||
<math>\sqrt{\frac{1}{N}\sum_{i=1}^{N}\left[g\left(t_{i}\right)\right]^{2}}=\sqrt{\sum_{k=0}^{N/2}\mid C_{k}\mid^{2}}</math>…………………………(C.5) | |||
g(t<sub>i</sub>)—— 时域函数在采样点的值;t<sub>i</sub>=i×T<sub>w</sub>/N 。 式(C.5) 表明,信号通过采样和数字化,其频域 分量的方均根值等于它在时域中的方均根值。在某些特定的情况下,可利用帕斯瓦尔关 系式来确定功率频谱是否能准确地描述时域信号。 | |||
g(t | |||
在上述设定的理想条件下,由本部分给定方法计算出的功率频谱是被测信号在指定的时间窗内各 频谱分量的平均功率。这种功率频谱准确地反映了被测信号的总功率、各单一频率分量的功率及其频 率。在实际情况下,当被测信号的所有分量确实是“基础”频率fw=1/T 的谐波时,这种理想的条件才 存在。由于本部分对同步有严格的要求,这种近于理想的条件仅在电力系统的基波频率和其他频率分 量为基础频率的整数倍时才出现,当然,也包括了信号分量为基波频率的谐波的情况。 | 在上述设定的理想条件下,由本部分给定方法计算出的功率频谱是被测信号在指定的时间窗内各 频谱分量的平均功率。这种功率频谱准确地反映了被测信号的总功率、各单一频率分量的功率及其频 率。在实际情况下,当被测信号的所有分量确实是“基础”频率fw=1/T 的谐波时,这种理想的条件才 存在。由于本部分对同步有严格的要求,这种近于理想的条件仅在电力系统的基波频率和其他频率分 量为基础频率的整数倍时才出现,当然,也包括了信号分量为基波频率的谐波的情况。 | ||
| 第1,125行: | 第1,071行: | ||
注:“基础”频率是时间窗宽度的倒数,“基波”频率是电源系统周期的倒数。 | 注:“基础”频率是时间窗宽度的倒数,“基波”频率是电源系统周期的倒数。 | ||
按照IEC61000-4-7 的第1版本的要求,当时的测量仪器设计中,时间窗的宽度是按16个周波来确 定的(≈320 ms 或≈267 ms) 。 将来设计测量仪器时,时间窗的宽度 | 按照IEC61000-4-7 的第1版本的要求,当时的测量仪器设计中,时间窗的宽度是按16个周波来确 定的(≈320 ms 或≈267 ms) 。 将来设计测量仪器时,时间窗的宽度 T<sub>w</sub>≈200 ms,是按系统频率为 50 Hz或60 Hz 时分别取10或12个周波来确定的。因此,频谱分量间的频率间隔(基础频率f<sub>w</sub>) 分别 ≈5 Hz 、≈3.125 Hz或≈3.75 Hz 。根据本部分的式(8)所给出的分群方法能确保准确地计算信号的总 功率。它不仅包括基波频率整数倍的(谐波)分量,而且考虑到了所有的频谱分量。式(8)是仅按频谱分 量间的频率间隔≈5 Hz 给出的,因此,当采用其他“基础”频率时,该公式要作修改。在理想条件下,帕 斯瓦尔关系式描述的功率频谱就可以准确地反映被测信号的平均功率,必要时应作上述修正。 | ||
在不太理想的情况下,如信号含有频率为 | 在不太理想的情况下,如信号含有频率为 f≠k×f<sub>w</sub>(k 是整数)的非谐波信号的成分,由于频率泄 漏现象引起频率信息损失,但信号功率通常能准确地描述。对于时间窗等于200 ms 的情况而言,只要 存在不是5 Hz 整数倍频率的间谐波信号(如287 Hz), 或者在分析的时间窗内信号幅值有波动,就会出 现非谐波的信号成分。本部分给出的分群方法有助于确保在大部分情况下能准确评估总功率。至于功 率如何分配到某个特定的信号组,那就取决于被测信号的特性了。 | ||
以下几个示例会有助于说明这一点。C.3 中的示例说明了电压、电流信号幅值波动的影响。C.4 中 说明了间谐波的影响。为了在图中以全屏的尺寸更加清楚地显示频谱线和分群的作用,在电压、电流信 号中实际上占有主导地位的基波分量被省略了。 | 以下几个示例会有助于说明这一点。C.3 中的示例说明了电压、电流信号幅值波动的影响。C.4 中 说明了间谐波的影响。为了在图中以全屏的尺寸更加清楚地显示频谱线和分群的作用,在电压、电流信 号中实际上占有主导地位的基波分量被省略了。 | ||
C.3 谐 波 的 波 动 | === C.3 谐 波 的 波 动 === | ||
示例1: | 示例1: | ||
| 第1,137行: | 第1,083行: | ||
图 C.1 表示的是5次谐波电流方均根值从3.536 A 波动至0.7071A 的例子。电流的阶跃是在21.25个5次谐波周 期之后出现的。对于这个例子,预期的电流方均根计算值应是2.367 A。但测得的5次谐波(单一频谱)结果仅为1.909 A, 即忽略了其他频谱分量产生了19.3%的误差。在这个例子中,谐波子群的测量值为2.276 A, 其误差已减少到3.84%,但谐波群的测量值为2.332 A, 相应的误差小至仅为1.47%。 | 图 C.1 表示的是5次谐波电流方均根值从3.536 A 波动至0.7071A 的例子。电流的阶跃是在21.25个5次谐波周 期之后出现的。对于这个例子,预期的电流方均根计算值应是2.367 A。但测得的5次谐波(单一频谱)结果仅为1.909 A, 即忽略了其他频谱分量产生了19.3%的误差。在这个例子中,谐波子群的测量值为2.276 A, 其误差已减少到3.84%,但谐波群的测量值为2.332 A, 相应的误差小至仅为1.47%。 | ||
[[文件:电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017_图C.1.5次谐波电流大波动.jpeg]] | [[文件:电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017_图C.1.5次谐波电流大波动.jpeg|400px]] | ||
图 C.1 5 次谐波电流大波动 | 图 C.1 5 次谐波电流大波动 | ||
| 第1,147行: | 第1,092行: | ||
[[文件:电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017_图C.2 5次谐波电压大波动.jpeg]] | [[文件:电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017_图C.2 5次谐波电压大波动.jpeg|400px]] | ||
| 第1,157行: | 第1,102行: | ||
[[文件:电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017_图C.3 某微波器具波动的3次谐波电流.jpeg]] | [[文件:电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017_图C.3 某微波器具波动的3次谐波电流.jpeg|400px]] | ||
| 第1,170行: | 第1,115行: | ||
通信(信号传输)系统也会加载在电力系统上。为了避免受到谐波的干扰,它们所采用的频率通常介于两个谐波频 率之间,即间谐波频率。如果它们的频率是“基本频率”f 的整数倍,并在时间窗内又有恒定的幅值,那么,频谱只是在 该频率上显示一条附加的频谱分量,而并不一定需要额外的分群。但是,为了传递信息,信号需要调制。这时对频谱的 影响与前面几个示例相似,仅有的差异只是从调制信号得到的频谱分量是以信号传输频率为中心的一组频谱分量。按 附录A 介绍的“间谐波群”的方法,可以按 C.3 中谐波分群方法减少误差。 | 通信(信号传输)系统也会加载在电力系统上。为了避免受到谐波的干扰,它们所采用的频率通常介于两个谐波频 率之间,即间谐波频率。如果它们的频率是“基本频率”f 的整数倍,并在时间窗内又有恒定的幅值,那么,频谱只是在 该频率上显示一条附加的频谱分量,而并不一定需要额外的分群。但是,为了传递信息,信号需要调制。这时对频谱的 影响与前面几个示例相似,仅有的差异只是从调制信号得到的频谱分量是以信号传输频率为中心的一组频谱分量。按 附录A 介绍的“间谐波群”的方法,可以按 C.3 中谐波分群方法减少误差。 | ||
在许多情况下,传输使用的信号都不是f<sub>w</sub>整数倍的频率。例如,图C.4 显示一个方均根值保持为23 V、频率为178 Hz 的通信信号迭加在系统中本已存在的3次和5次谐波(幅值均为11.5 V) 之上。尽管离散傅立叶变换不能直接分解出 178 Hz的功率,它却能把功率分散到该频率的临近的频谱分量上(所谓的“泄漏”)。这时,3、5次谐波之间的间谐波组 (参见附录A)收集了该通信信号分散功率的主要部分,得到的值为22.51 V,误差只有2.15%。 | |||
[[文件:电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017_图C.4 178Hz的通信信号以及3次、5次谐波.jpeg]] | [[文件:电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017_图C.4 178Hz的通信信号以及3次、5次谐波.jpeg|400px]] | ||
| 第1,180行: | 第1,125行: | ||
注1:对于频率为非“基本频率”整数倍的信号来说,其“泄漏”效应就是在原有的谐波矢量上添加了一个附加矢量 (见图C.7) 。 同一频率的附加矢量与原始谐波矢量之间的相位角在各个时间窗中的增加(或减少)几乎相等。 合成矢量的大小则根据实际相位角的不同在这两个矢量差及矢量和的幅值之间变化。在所给的示例中,原始 谐波矢量的大小为11.5 V,150 Hz时≈1.2 V、250 Hz时≈0.4 V (见图 C.4),则合成矢量的大小对于150 Hz 在≈10.3 V 和≈12.7V 之间变化,对于250 Hz 在≈11.1V 和≈11.9 V 之间变化。由许多个毗邻时间窗得到 的合成矢量的方均根值等于原始谐波矢量与附加矢量共同的方均根值,该例中150 Hz 时11.56 V 、250 Hz | 注1:对于频率为非“基本频率”整数倍的信号来说,其“泄漏”效应就是在原有的谐波矢量上添加了一个附加矢量 (见图C.7) 。 同一频率的附加矢量与原始谐波矢量之间的相位角在各个时间窗中的增加(或减少)几乎相等。 合成矢量的大小则根据实际相位角的不同在这两个矢量差及矢量和的幅值之间变化。在所给的示例中,原始 谐波矢量的大小为11.5 V,150 Hz时≈1.2 V、250 Hz时≈0.4 V (见图 C.4),则合成矢量的大小对于150 Hz 在≈10.3 V 和≈12.7V 之间变化,对于250 Hz 在≈11.1V 和≈11.9 V 之间变化。由许多个毗邻时间窗得到 的合成矢量的方均根值等于原始谐波矢量与附加矢量共同的方均根值,该例中150 Hz 时11.56 V 、250 Hz 时11.51V 。 分群之后的平滑过程使结果的变化大大减少,并给出了一个接近于共同的方均根值的平均输出量。 注2:实际上,通信信号的幅值比本例中所述的要小,所以,它的“泄漏”效应将相应地减小。 | ||
示例2: | 示例2: | ||
| 第1,189行: | 第1,132行: | ||
[[文件:电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017_图C.5287Hz的间谐波以及5次和6次谐波.jpeg]] | [[文件:电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017_图C.5287Hz的间谐波以及5次和6次谐波.jpeg|400px]] | ||
图 C.5 287 Hz 的 间 谐 波 以 及 5 次 和 6 次 谐 波 | 图 C.5 287 Hz 的 间 谐 波 以 及 5 次 和 6 次 谐 波 | ||
| 第1,197行: | 第1,140行: | ||
如图 C.6a)所示, 一个变转矩的电子式马达驱动(例如活塞泵)会在供电系统中产生5次谐波,其幅值有5 Hz、20% 的正弦调制,围绕平均方均根值10V 波动。时域函数在0.2 s 时间内的总方均根值评估为10.10 V 。其频谱中的250 Hz 频率含有一根方均根值为10 V 的“载波”分量,并在两侧频率245 Hz 和255 Hz 各有 一 根1 V 分量,见图C.6c)。250 Hz 处单根频谱分量的误差为0.99%;而由谐波子群得到的结果就没有误差了。 | 如图 C.6a)所示, 一个变转矩的电子式马达驱动(例如活塞泵)会在供电系统中产生5次谐波,其幅值有5 Hz、20% 的正弦调制,围绕平均方均根值10V 波动。时域函数在0.2 s 时间内的总方均根值评估为10.10 V 。其频谱中的250 Hz 频率含有一根方均根值为10 V 的“载波”分量,并在两侧频率245 Hz 和255 Hz 各有 一 根1 V 分量,见图C.6c)。250 Hz 处单根频谱分量的误差为0.99%;而由谐波子群得到的结果就没有误差了。 | ||
在同一个系统中可加载频率为287 Hz、幅值为9.8 V 的通信信号[见图C.6b]]。 该信号在以200 ms 时间窗内的周 期数为57.4次,是非整数,从而在频谱中出现“泄漏”效应(见图 C.6d)] 。 由间谐波群得到的方均根值为9.538 V, 误差为 2.7%。 | 在同一个系统中可加载频率为287 Hz、幅值为9.8 V 的通信信号[见图C.6b|400px]]。 该信号在以200 ms 时间窗内的周 期数为57.4次,是非整数,从而在频谱中出现“泄漏”效应(见图 C.6d)] 。 由间谐波群得到的方均根值为9.538 V, 误差为 2.7%。 | ||
当波动的谐波和通信信号同时加载在电压上时[见图 C.6e]], 总的方均根值为14.07 V 。所得到的频谱分量可用不 同的组合方式加以组合[见图C.6f]] 。 因为在250 Hz 存在谐波,而且从频谱的包络线来看在285 Hz 附近有明显的信 号,用两个群的方式就合理一些(但每个频谱分量只能用一次): | 当波动的谐波和通信信号同时加载在电压上时[见图 C.6e|400px]], 总的方均根值为14.07 V 。所得到的频谱分量可用不 同的组合方式加以组合[见图C.6f|400px]] 。 因为在250 Hz 存在谐波,而且从频谱的包络线来看在285 Hz 附近有明显的信 号,用两个群的方式就合理一些(但每个频谱分量只能用一次): | ||
——9.36V 的间谐波群(相对于9.8 V 的误差为4.5%)和一根10. 16 V 的谐波频谱分量(相对于10.0 V 的误差为 1.6%),结果是总的方均根值为13.81 V (相对于14.07 V 的误差为1.8%); | ——9.36V 的间谐波群(相对于9.8 V 的误差为4.5%)和一根10. 16 V 的谐波频谱分量(相对于10.0 V 的误差为 1.6%),结果是总的方均根值为13.81 V (相对于14.07 V 的误差为1.8%); | ||
——9.34 V的间谐波子群(相对于9.8V 的误差为4.7%)和10.23 V 的谐波子群(相对于10.1V 的误差为1.29%), | |||
结果得到总的方均根值为13.85 V(相对于14.07 V 的误差为1.5%)。 | 结果得到总的方均根值为13.85 V(相对于14.07 V 的误差为1.5%)。 | ||
| 第1,209行: | 第1,152行: | ||
第2种组合方式更符合“物理意义”,因为245 Hz 和255 Hz 的频谱分量并不在“泄漏”的包络线之中。如果注意观 察几个毗邻的时间窗的频谱的话,这一点就很清楚了。 | 第2种组合方式更符合“物理意义”,因为245 Hz 和255 Hz 的频谱分量并不在“泄漏”的包络线之中。如果注意观 察几个毗邻的时间窗的频谱的话,这一点就很清楚了。 | ||
[[文件:电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017_图C.6 调制后的5次谐波和频率为287Hz的间谐波.jpeg|400px]] | |||
[[文件:电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017_图C.6 调制后的5次谐波和频率为287Hz的间谐波.jpeg]] | |||
图 C.6 调制后的5次谐波和频率为287 Hz 的 间 谐 波 | 图 C.6 调制后的5次谐波和频率为287 Hz 的 间 谐 波 | ||
5次谐波两侧旁带得到的频谱分量主要是泄漏效应的结果。对于一个波动的谐波来说,谐波旁带频率(即245 Hz 和255 Hz) 分量的矢量,其大小相等,方向相反。矢量的大小在恒定的调制深度下保持不变。但是,如果调制频率不是 基本频率的整数倍,其角度从一个时间窗到下一个时间窗会一步一步地旋转。由频率为287 Hz 的间谐波得到的矢量的 大小也几乎保持不变,但因为该间谐波在时间窗中的位置在改变,所以对各个时间窗来说该间谐波矢量的角度在改变。 当然,由调制和泄漏合成的矢量,其大小和角度在不同的时间窗内也在改变。图C.7 表 示 的 是 图 C.6 所示的时间窗内 5次谐波上下各5 Hz 的分量。这时,相对于“调制”矢量来说,245 Hz 的合成幅值是增加了,而255 Hz 的合成幅值是减 小了。在其他的时间窗内由287 Hz 的信号产生的矢量就有其他的角度,相应的合成矢量的幅值也就不同。频谱的时间 表示方式在245 Hz 和255 Hz 处显示出频谱分量的波动,而该时间段的平均值却近似于“调制”和“泄漏”矢量的共同的 方均根值。 | 5次谐波两侧旁带得到的频谱分量主要是泄漏效应的结果。对于一个波动的谐波来说,谐波旁带频率(即245 Hz 和255 Hz) 分量的矢量,其大小相等,方向相反。矢量的大小在恒定的调制深度下保持不变。但是,如果调制频率不是 基本频率的整数倍,其角度从一个时间窗到下一个时间窗会一步一步地旋转。由频率为287 Hz 的间谐波得到的矢量的 大小也几乎保持不变,但因为该间谐波在时间窗中的位置在改变,所以对各个时间窗来说该间谐波矢量的角度在改变。 当然,由调制和泄漏合成的矢量,其大小和角度在不同的时间窗内也在改变。图C.7 表 示 的 是 图 C.6 所示的时间窗内 5次谐波上下各5 Hz 的分量。这时,相对于“调制”矢量来说,245 Hz 的合成幅值是增加了,而255 Hz 的合成幅值是减 小了。在其他的时间窗内由287 Hz 的信号产生的矢量就有其他的角度,相应的合成矢量的幅值也就不同。频谱的时间 表示方式在245 Hz 和255 Hz 处显示出频谱分量的波动,而该时间段的平均值却近似于“调制”和“泄漏”矢量的共同的 方均根值。 | ||
[[文件:电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017_图 C.7频率分别为245和255I处的矢量.jpeg|400px]] | |||
[[文件:电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017_图 C.7频率分别为245和255I处的矢量.jpeg]] | |||
图 C.7 频 率 分 别 为 2 4 5 Hz 和 2 5 5 Hz 处 的 矢 量 | 图 C.7 频 率 分 别 为 2 4 5 Hz 和 2 5 5 Hz 处 的 矢 量 | ||
2025年6月12日 (四) 17:24的最新版本
引用资料
文件:电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017.pdf
标准状态
当前标准:电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017
发布日期:2017-07-12
实施日期:2018-02-01
旧标准:电磁兼容 试验和测量技术 供电系统及所连设备谐波、谐间波的测量和测量仪器导则GB/T 17626.7-2008
发布日期:2008-05-20
实施日期:2009-01-01
废止日期:2018-02-01
1 范围
GB/T 17626的本部分适用于测量叠加在50 Hz 或60 Hz 电力系统基波上的频谱分量(最高 9kHz) 的测量仪器。从实际应用考虑,本部分将信号分为谐波、间谐波以及其他高于谐波范围但低于 9 kHz 的分量。
本部分规定了可用于根据某些标准中给出的发射限值(例如 IEC 61000-3-2 中给出的谐波电流限 值)对设备逐项进行试验,以及对实际供电系统中谐波电流和电压的测量的仪器。对谐波频率以上至 9 kHz范围的测量仪器,做了暂行规定(参见附录 B) 。 对间谐波产生和测量以及特殊测量方法做了暂 行规定,(参见附录 C)。
注1:本部分涉及的仪器是基于离散傅立叶变换的。
注2:本部分清晰地描述了测量仪器的结构和功能,因此可按字面意思理解。这是因为无论输人信号特性如何,均 要求参考仪器都能得到重复结果。
注3:规定的测量仪器需具有测量最高为50次谐波的能力。
2 规范性引用文件
下列文件对于本文件的应用是必不可少的。凡是注日期的引用文件,仅注日期的版本适用于本文 件。凡是不注日期的引用文件,其最新版本(包括所有的修改单)适用于本文件。
IEC 60038 标准电压(Standard voltages)
IEC 60050-161 国际电工词汇(IEV) 第161章:电磁兼容[International Electrotechnical Vocab- ulary(IEV)—Chapter 161:Electromagnetic compatibility]
IEC 61000-2-2 电磁兼容(EMC) 第2部分:环境 第2分部分:公用低压供电系统低频传导骚 扰及信号传输的兼容水平[Electromagnetic compatibility(EMC)-Part 2:Environment—Section 2: Compatibility levels for low-frequency conducted disturbances and signalling in public low-voltage power supply systems]
IEC 61000-3-2 电磁兼容(EMC) 第3-2部分:限值 谐波电流发射限值(设备每相输入电流≤ 16 A)[Electromagnetic compatibility(EMC)-Part 3-2:Limits—Limits for harmonic current emissions(equipment input current≤16A per phase)]
IEC 61000-3-12 电磁兼容(EMC) 第3-12部分:限值(每相输入电流大于16 A 小于等于75 A) 连接到公用低压系统的设备产生的谐波电流限值[Electromagnetic compatibility(EMC)-Part 3-12: Limits—Limits for harmonic currents produced by equipment connected to public low-voltage systems with input current >16A and≤75 A per phase]
3 术语和定义
IEC 60050-161(IEV)中界定的及以下术语和定义适用于本文件。
3.1 有关频率分析的定义
工程上对于信号分析通常采用三角形式的傅立叶级数展开法,即频率分析法,这样比较容易通过过 零点观察测量相角。傅立叶级数展开式定义于如式(1)所示,f(t)可代表任意一个周期信号。
[math]\displaystyle{ f(t)=c_{0}+\sum_{k=1}^{\infty}c_{k}\sin\left(\frac{k}{N}\omega_{1}t+\varphi_{k}\right) }[/math]…………………………(1)
式(1)中的相关参数见式(2)。
[math]\displaystyle{ \begin{aligned} & c_{k}=\mid b_{k}+ja_{k}\mid=\sqrt{a_{k}^{2}+b_{k}^{2}} \\ & Y_{\mathrm{c},k}=\frac{c_{k}}{\sqrt{2}} \end{aligned} }[/math]
[math]\displaystyle{ \varphi_k=\pi+\arctan\left(\frac{a_k}{b_k}\right),\text{若 }b_k\lt 0\quad\varphi_k=\arctan\left(\frac{a_k}{b_k}\right),\text{若 }b_k\gt 0\varphi_k=\frac{\pi}{2}\text{,若 }b_k=0\text{ 且 }a_k\gt 0\quad\varphi_k=-\frac{\pi}{2}\text{,若 }b_k=0\text{ 且 }a_k\lt 0 }[/math]
………(2)
其 中 ɛ=0.05%Um,ɛ=0.15%Imm 或 ɛ=0.15%Uno,ɛ=0.5%Inom
分别参见IEC 61000-4-7的 表 1
式(2)中的相关参数见式(3)。
[math]\displaystyle{ \begin{aligned} & b_{k}=\frac{2}{T_{N}}\int_{0}^{T_{N}}f\left(t\right)\times\sin\left(\frac{k}{N}\omega_{1}t\right)\mathrm{d}t \\ & a_{k}=\frac{2}{T_{N}}\int_{0}^{T_{N}}f\left(t\right)\times\cos\left(\frac{k}{N}\omega_{1}t\right)\mathrm{d}t \\ & c_{0}=\frac{1}{T_{N}}\int_{0}^{T_{N}}f\left(t\right)\mathrm{d}t \end{aligned} }[/math]
…………………………(3)
注1:以上定义中将bk 与ak 很小情形下的φ设置为0,为仪器制造商提供了指导。由于幅值很小时的相位测量的 偏差可能非常大,因此这类小信号无需测量相位。
式中:
W1 ——基波角频率(wi=2πfH,1), 单位为弧度每秒(rad/s);
TN—— 时间窗的宽度(持续时间);时间窗是在一个时域函数上进行傅立叶变换的时间段,单位为 秒(s);
co— 直流分量;
Ck—— 频率为fc,k=kfa,1/N 的分量的幅值;
Yc,k——分 量c 的方均根值;
fH,1—— 电力系统基波频率,单位为赫兹(Hz);
k ——与频率分辨率(fc,=1/Tn) 相关的序数(频谱分量的次序);
N ——时间窗宽度内的基波周期数,单位是个;
φk ——频谱分量k 的相角,单位为弧度(rad)。
注2:严格地讲,这些定义仅适用于稳态信号。在多数情况下,傅立叶级数实际上通过数字信号进行分析,即离散傅 立叶变换(DFT)或快速傅立叶变换(FFT)。
对待分析的模拟信号f(t)进行采样,经A/D 变换并存储。每组M 个样本构成一个时间窗,并在该时间窗上进行 DFT。 根据傅立叶级数展开式,时间窗口宽度TN 决定了频率的分辨率fc,1=1/Tn (即频谱分量的频率间隔)。因此,窗 口宽度Tn应是系统电压基波周期T1的 N 个整数倍:TN=N×T₁ 。 此时采样频率为f=M/(NT₁) (式中,M 为时间 窗TN内的样本数)。
在进行DFT 之前,在时间窗 TN之内的样本通常要乘以一个特殊的对称函数“窗函数”进行加权。如果对周期性信 号进行同步采样,对每一个样本乘以权重为1的矩形加权窗函数则更可取。
DFT 变换后的频谱分量频率fc,k=k/TN(k=0,1,2,…,M-1), 含有正交的傅立叶系数a 和b 。 然而,式中仅k≤M/2 的值是有用数据,后面一半数据只是重复。
在同步采样条件下,与基波频率fH,1 相关的谐波次数为h 的分量,在频谱序列上表示为 k=hN 的频谱分量。
注3:快速傅立叶变换(FFT) 是一种可以缩短计算时间的特殊算法。它要求样本数 M 是2的整数次幂,即 M= 2i,如i≥10。
注4:甄别不同的信号,可以用符号I 替代Y 来表示电流,用符号U 代替Y 来表示电压,下标C 则限定为频谱分量。
3.2 有关谐波的定义
3.2.1
谐波频率 harmonic frequency
fH,h
电力系统(基波)频率的整数倍频率,fH,h=h×fH,1。
注:k=hN 时,谐波频率fH.h与频谱分量的频率fc, 相等。
3.2.2
谐波次数 harmonic order
h
谐波频率与电力系统基波频率的(整数)比。 DFT 分析中,当基波频率fH,1 与采样频率f, 同 步 时 , 谐波次数h 对应的频谱分量k=h×N(k 为频谱分量的次数,N 为时间窗 TN 内的基波频率周期数)。 3.2.3
谐波分量的方均根值 r.m.s.value of a harmonic component
YH,h
非正弦波形经过 DFT 分析后得到的谐波频率分量的方均根值。
为表达上的简明扼要,这样的一个分量可简称“谐波”。
注1:谐波分量YH,A等于频谱分量Yc,k,k=h×N;(YH,A=Yc,hxN) 。 甄别不同的信号,可以用符号I 替代Y 表 示电流,用符号U 代替Y 表示电压。下标 H 则表示 I 或U 的分量为谐波。
注2:为了实现本部分的目标,时间窗采用N=10(50 Hz系统)或N=12(60 Hz系统)个基波周期的宽度,即大约 为200 ms(见4.4.1),因此YH,h=Yc,1o×h(50 Hz系统)或YH,=Yc,12xh(60 Hz系统)。
3.2.4
谐波群的方均根值 r.m.s.value of a harmonic group
Yg,h
某一次谐波方均根值和在时间窗之内与两侧相邻的频谱分量的方均根值之和的平方根值,如此把 谐波能量以及两侧相邻各频谱分量的能量值累加在一起。见式(8)和图4。谐波群的次数则为所考虑 的谐波次数。
注:用符号I 替代Y 则表示电流,符号 U 代替Y 则表示电压。
3.2.5
谐波子群的方均根值 r.m.s.value of a harmonic subgroup
Ysg,h
指某一谐波方均根值和与之两侧紧邻的两个频谱分量的方均根值之和的平方根值。在电压测量过 程中,考虑到电压波动的影响,将DFT 输出的谐波能量加上紧邻其两侧的两个频率分量的能量,得到一 个子群[见式(9)和图6]。谐波子群的次数即为所考虑的谐波次数。
注:用符号I 替代Y 则表示电流,符号U 代替Y 则表示电压。
3.3 有关畸变因数的定义
3.3.1
总谐波畸变率 total harmonic distortion
THD
THDY ( 符 号 )
不 大 于 指 定 次 数(hmax) 的 所 有 谐 波 分 量YH,h 的 方 均 根 值 与 基 波 分 量YH, 方均根值的比值,见 式(4):
[math]\displaystyle{ THD_{Y}=\sqrt{\sum_{h=2}^{h_{\max}}\left(\frac{Y_{H,h}}{Y_{H,1}}\right)^{2}} }[/math]…………………………(4)
注1:用符号I 替代Y 则表示电流,单位为安培(A); 符号 U 代替Y 则表示电压,单位为伏特(V)。
注2:如果在相关现值标准(如IEC 61000-3系列标准)中,没有规定其他值,则hmax取值为40。
3.3.2
谐波群的总畸变率 group total harmonic distortion
THDG
THDGY ( 符 号 )
谐 波 群Yg,h 的方均根值与基波群Yg,1的方均根值的比值,见式(5)。
[math]\displaystyle{ THDG_{Y}=\sqrt{\sum_{h=h_{\mathrm{min}}}^{h_{\mathrm{max}}}\left(\frac{Y_{g,h}}{Y_{g,1}}\right)^{2}},\text{其中 }h_{\mathrm{min}}\geqslant2 }[/math]…………………………(5)
注1:用符号I 替代Y 则表示电流,单位为安培(A); 符号U 代替Y 则表示电压,单位为伏特(V)。
注2:如果有关限值的标准(例如在IEC 61000-3系列标准中)未标定其他值,则hmax 取值40,h 取值2。 3.3.3
谐波子群的总畸变率 subgroup total harmonic distortion
THDS
THDSy ( 符 号 )
谐 波 子 群Ysg,h 的方均根值与基波子群Ysg,1D 的方均根值的比值,见式(6)。
[math]\displaystyle{ THDS_{Y}=\sqrt{\sum_{h=h_{\mathrm{min}}}^{h_{\mathrm{max}}}\left(\frac{Y_{sg,h}}{Y_{sg,1}}\right)^{2}}\quad h_{\mathrm{min}}\geqslant2 }[/math]…………………………(6)
注1:用符号I 替 代Y 则表示电流,单位为安培(A); 符号U 代替Y 则表示电压,单位为伏特(V)。
注2:如果有关限值的标准(例如在IEC 61000-3系列标准中)未标定其他值,则hmax取值40,hm 取值2。 3.3.4
部分谐波加权畸变率 partial weighted harmonic distortion
PWHD
PWHDH,Y ( 符 号 )
某 一 范围高次谐波(从hmin次 到hmax 次谐波)的方均根值与基波方均根值的比值,并用谐波次数h 加权,见式(7)。
[math]\displaystyle{ PWHD_{\mathrm{H},Y}=\sqrt{\sum_{h=h_{\mathrm{min}}}^{h_{\mathrm{max}}}h\left(\frac{Y_{\mathrm{H},h}}{Y_{\mathrm{H},1}}\right)^{2}} }[/math]…………………………(7)
注1:用符号I 替 代Y 则表示电流,单位为安培(A); 符号U 代替Y 则表示电压,单位为伏特(V)。
注2:引入部分谐波加权畸变率的概念是为了给高次谐波分量的集合规定一个限值。可通过用量值Yg,h 代 替YH,A 来评估部分谐波群加权畸变率PWHDg,y; 可通过用量值Ysg,h 代 替YH,A 来评估部分谐波子群加权畸变率 PWHDsg,y 。 相关标准(IEC 61000-3系列)在使用PWHD 类 型(PWHDH,y,PWHDg,Y, 或 PWHDsg,Y) 的限 值时,均对其有定义。
注3:相关标准(IEC 61000-3系列)在使用PWHDY 时,均对 hmin 和 hmax 的值做了定义。
3.4 有关间谐波的定义
3.4.1
频谱分量的方均根值 r.m.s.value of a spectral component
Yc,k
在对波形进行分析后的各频谱分量方均根值,其频率为采样窗口时间倒数的整数倍。
注1:如果时间窗持续时间数倍于基波周期,仅有某些频谱分量的频率为基波频率的整数倍。
注2:两个连续频谱分量间的频率间隔为时间窗宽度的倒数,本部分中大约为5 Hz。
注3:用符号 I 替代Y 则表示电流,单位为安培(A); 符号U 代替Y 则表示电压,单位为伏特(V)。
3.4.2
间谐波分量的方均根值 r.m.s.value of an interharmonic component
Yc,i
介于两个相邻谐波频率之间的某一频谱分量YC,k≠hxn 的方均根值(见图4),为简明扼要起见,该分 量可简称为“间谐波”。
注1:间谐波分量的频率由谱线的频率给定,该频率不是基波频率的整数倍。
注2:设备产生的实际“间谐波分量”(如频率为183.333 Hz),与由仪器对波形测量分析计算得出的“频谱分量”(如 50 Hz系统,FFT 频谱中的频率185 Hz 分量)之间有差异。当频率为h×N(h 为整数),“频谱分量”同时也 是“谐波分量”。
3.4.3
间谐波群的方均根值 r.m.s.value of an interharmonic group
Yig,h
指在两个相邻谐波频率之间所有频谱分量的方均根值(见图4)。
注1:为便于表述,谐波次数在h 和h+1 之间的间谐波群的方均根值指定为Yg,h。例如,在 h=5 和 h=6 之间的 间谐波群指定为Yig,5。
注2:用符号 I 替代Y 则表示电流,单位为安培(A); 符号U 代替Y 则表示电压,单位为伏特(V)。
3.4.4
间谐波中心子群的方均根值 r.m.s.value of an interharmonic centred subgroup
Yisg,h
在两个相邻谐波频率之间,全部频谱分量(但不包括与谐波频率直接相邻的两个频谱分量)的方均 根值(见图6)。
注1:为便于表述,谐波次数在h 和h+1 之间的间谐波中心子群的方均根值指定为Ygh 。 例如,在 h=5 和 h=6 之间的间谐波中心子群指定为Yisg,5。
注2:用符号I 替代Y 则表示电流,单位为安培(A); 符号U 代替Y 则表示电压,单位为伏特(V)。
3.4.5
间谐波群频率 interharmonic group frequency
fig,h
指间谐波群两侧的两个谐波频率的平均值,即 fig,h=(fH,h+fH,h+1)/2。
3.4.6
间谐波中心子群频率 interharmonic centred subgroup frequency
fisg,h
该间谐波子群两侧的两个谐波频率的平均值,即fisg,h=(fH,h+fH,h+1)/2。
3.5 符号
3.5.1 符号与缩写
下列缩略语适用于本部分。除非特别声明,本部分中,电压和电流值是指方均根值。
a 傅立叶级数中余弦分量系数的幅值
b 傅立叶级数中正弦分量系数的幅值
c 傅立叶级数系数的幅值
f 频率;函数
fc,k k 次频谱分量
fc,1 1 次频谱分量,频率的分辨率等于该频率
fg,h h 次谐波群频率
fsg,h h 次谐波子群频率
fig,h h 次间谐波群频率
fisg,h h 次间谐波中心子群频率
fH,h h 次谐波分量频率
fH,1 电力系统基波频率
f₅ 采样率
hmax 所考虑的最高谐波次数
hmin 所考虑的最低谐波次数
j √-1
t 运行时间
B 带宽
I 电流(方均根值)
M 整数,时间窗内采集的样本数
N 时间窗宽度内供电电源的周期数 P 功率
T 时间间隔
T1 供电系统的基波周期
TN 时间窗宽度含有的N 个基波周期
U 电压(方均根值)
Y 可由I、U 代替的变量
Yc, k 次频谱分量的方均根值
Yg,h 谐波群的方均根值
YH,h h 次谐波分量的方均根值
Yig,h 间谐波群的方均根值
Yisg,h 间谐波中心子群的方均根值
Ysg,h 谐波子群的方均根值
W 角频率
w1 供电系统的基波角频率
φ 相位角
3.5.2 下标
下列下标适用于本部分。
b 中心带频率
h 标识谐波次数的整数序列号
k 标识频谱分量的整数序列号
m 测量值
max 最大值
min 最小值
0 平滑值 g 群值
sg 子群值
i 间谐波值
g,h 与h 次谐波相关的谐波群次数
sg,h 与h 次谐波相关的谐波子群次数
sg,1 与基波相关的谐波子群次数
ig,h h 次谐波上方的间谐波群
isg,h h 次谐波上方的间谐波中心子群
og,h 平滑后的h 次谐波群
nom 标称值
S 采样的标识
C 与频谱分量相关的值
H 谐波
f 频率
0 与直流分量相关的
4 各类型测量仪器的通用概念和共同要求
4.1 被测信号的特性
仪器应考虑到用于下列类型的测量:
a) 谐波发射的测量;
b) 间谐波发射的测量;
c) 谐波频率以上至9 kHz 范围的测量。
严格地讲,只有在稳态信号下FFT 才能得到准确的结果,时变信号(信号随时间变化)仅仅用谐波 分量是不能对其准确描述的。当被测对象的电源波动、由此导致基波电流并且谐波电流也可能波动时, 为了获得重复性较好的谐波发射分析结果,应综合采用平均方法和足够长的测量周期。因此,本部分提 供了一种简化的方法,也就是特定的平均方法(见5.5.1)。另外,规范了足够长的试验观察周期,使获取 的连续测量结果的误差满足与本部分相对应的谐波发射标准。
4.2 仪器的准确度等级
在满足应用要求的前提下,允许使用简单而低成本的仪器,为此考虑了两类准确度(I 、Ⅱ) 。 在发射测试中,如果发射值接近限值,则要求使用更高准确度的I类仪器(见表1的注2)。
4.3 测量的类型
给出了用于谐波和间谐波测量的要求。也考虑了在最高至9 kHz 频率范围内信号的测量。
4.4 仪器的通用架构
新设计的仪器可能使用离散傅立叶变换(DFT), 通常采用一种称为快速傅立叶变换(FFT) 的算法。因此本部分仅考虑这种结构,但不排除其他分析原理(见第6章)。
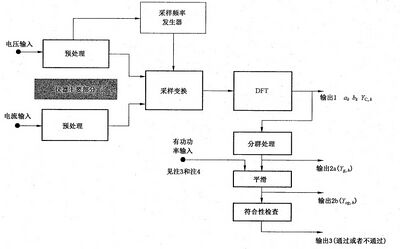
图1给出了仪器的通用架构。 一台仪器可以包括,也可以不包括图1所标示的全部模块和输出。
4.4.1 仪器的主要部分
仪器主要包括:
——具有抗混叠滤波器的输入回路;
——含有采样/保持单元的A/D 转换器; ——同步单元和窗函数单元(必要时);
——提供傅立叶系数a 和b 的 DFT 处理器("输出1")。
仪器可增加电流和/或电压评价的特殊单元。
注 1 : 更 详 细 的 信 息 可 参 见 5 . 5 。
注2:为分析谐波和间谐波,将待分析信号 f(t) 进行预处理,以消除高于仪器处理范围的频率。
窗口宽度应为10(50 Hz 系统)或12(60 Hz 系统)个基波周期[TN=(10 或12)×T₁≈200 ms],
并带有矩形加权窗,并与电力系统的基波频率同步。汉宁窗加权仅在失去同步的情况下允许使用。这 种同步丢失应在仪器显示器上显示,并应标记此时得到的数据,不能据此数据判断标准符合性,但可用 于其他目的。
每一组10个或12个周期的时间窗应与50 Hz 或60 Hz 的电力系统频率同步。第一个采样脉冲和 第(M+1) 个采样脉冲的上升沿之间的时间(M 为样本数,见3.5.1),应等于电力系统特定周期数的持 续时间,最大允许误差为±0.03%。当被测信号的频率偏差在标称系统频率±5%之内时,含有锁相环 或其他同步方式的仪器,应满足准确度和同步要求。然而,对于由集成电源供电的仪器,因电源与测量 系统已同步,对工作输入频率范围的要求不再适用,只需满足同步和频率准确度的要求。
仪器的输出“输出1”(见图1)应能分别给出电流或电压在DFT 后的每一个系数 ak 和bk, 以及 Yc,k,即计算出的每一个频率分量的值。
图 1 测量仪器的通用架构
还要提供与谐波测量同一时间窗内的有功功率评估,但不一定来自DFT 分析。根据 IEC 61000-3-2 进行谐波发射测量时,这个功率不应包含直流分量。
注3:有功功率P 作为平滑过程的输入,无需分群处理。
注4:直流分量及直流功率的测量可以作为一个选件包括在仪器中,但本部分不作要求。
4.4.2 后处理部分
按发射标准的要求,对原始数据进行诸如平滑和原始结果的加权等的附加运算在仪器的后续部分 中进行。
如果将输出值与相应的数值(基波的声称值或标称值)作归一化处理,则应仅在这些附加的平滑过 程之后进行。
5 谐波测量
5.1 电流输入回路
电流输入回路应与待分析的电流相适应,应能对谐波电流进行直接测量。此外,还应有一个低压高 阻抗电压输入端,可以是外部的电阻分流器(或电流互感器与电阻分流器的组合)。合适的输入回路灵 敏度范围为0.1 V~10 V,如果输入回路满足5.3的要求,0.1 V 是优选值。
注:如果在电路中直接测量电流,建议(但不要求)提供以下输入电流Inom测量范围(方均根值):0.1A、0.2 A、0.5A、1A、2 A、5A、10 A、20 A、50 A、100 A。
Ⅱ类测量仪器中电流输入回路的功率损耗应不超过3 VA,I 类测量仪器输入回路电压降的方均 根值不应超过0.15 V。
每一个电流输入回路应能够承受1.2Inm 的连续输入电流,并在持续1s 的 10Inom 的电流应力下,不导致任何损坏。
信号方均根值不大于5A 时,仪器应能够接受峰值系数最高为4的输入信号;信号方均根值不大于 10A 时,峰值系数应达到3.5;更高的量程时,峰值系数应达到2.5。
要求仪器具备过载指示功能。
表1给出了所有准确度要求。
其他要求见第8章。
注:直流分量常与待测的畸变电流相关,这样的直流分量在输入电流互感器中会产生较大误差。制造商应在仪器 的技术规范中指出允许的最大直流分量,以保证因其引起的误差不超过规定的准确度。
5.2 电压输入回路
测量仪器的电压输入回路应适应待分析电压的最大值和频率,在电压信号幅值高达1.2倍的最大 电压值(量程)时,仍应能保持其性能和测量准确度不变。1.5以上的峰值系数才能满足测量要求;在电 压高度畸变的工业电网中,峰值系数至少取2才能满足测量要求。任何情况下都要求有过载指示。
在交流电压输入信号为4倍额定输入电压或1kV 的方均根值(取较小者),持续1s 的电压下,不 应引起仪器的任何损坏。
很多标称供电电压在60 V~690V 之间,这取决于当地实际情况。为使测量仪器能广泛适用于多 数供电系统,建议按照以下标称电压设计输入回路的档级:
Unom:对50 Hz 系统:66 V 、115V 、230 V 、400 V 、690V;
Unom:对60 Hz 系统:69 V 、120 V 、240V 、277V 、347V 、480 V 、600 V。
注1:利用外部电压互感器时,附加的电压范围(100V 、100/√3V 、110/√3 V)可能有利于应用。
注2:具备更高灵敏度的输入信号端子(0.1 V、1V、10 V)有助于利用外部传感器。输入回路应能承受的输入信号 峰值系数至少为2。
输入回路在230 V 时的功率损耗不应超过0.5 VA, 如果提供高灵敏度输入(低于50 V) 端子,其输 入电阻至少应为10 kΩ/V。
应注意,与要测量的其他电压分量相比,幅值很高的基波(供电频率)电压不应产生过载导致仪器损坏,或不应引起仪器输入端信号相互调制。这样引起的误差应低于规定的准确度。应有过载指示。
5.3 准确度要求
推荐将仪器测量谐波分量的准确度分为两级。在制造商标明的额定使用条件(温度范围、相对湿度 范围、仪器电源电压等)下,测量仪器在其工作频率范围内,对单一频率和稳态信号的最大允许误差见 表 1 。
注:当按IEC 61000-3-2测试设备时,其不确定度按此原则取较大值:允许限值(允许限值的5%),或被测设备的额定电流I, 相关(即0.15%Ir) 。 这在选择测量仪器的合适的输入电流量程时应加以考虑。
表 1 电流、电压和功率测量的准确度要求
| 准确度 | 测量类型 | 测量条件 | 最大误差 |
|---|---|---|---|
| I | 电压 | Um≥1%Unom Um<1%Unom |
±5%Um ±0.05%Unom |
| 电流 | Im≥3%Inom Im<3%Inom |
±5%Im ±0.15%Inom | |
| 功率 | Pm≥150 W Pm<150 W |
±1%Pm ±1.5W | |
| Ⅱ | 电压 | Um≥3%Unom Um<3%Unom |
±5%Um ±0.15%Unom |
| 电流 | Im≥10%Inom Im<10%Inom |
士5%Im ±0.5%Inom | |
| Inom:测量仪器的标称电流范围; Unom:测量仪器的标称电压范围; Um,Im和Pm:测量值。 | |||
| 注1:在诸如验证是否满足标准、解决争议等需要精确测量时,推荐使用I类仪器。任何满足I类要求的两台仪 器,在与同一信号相连时,会得到与规定准确度相符的结果(或显示过载状态)。 注2:I类仪器推荐用于发射测量。Ⅱ类仪器推荐用于常规普查,也可用于允许不确定度增大的情况下,测量结 果明显不会超过限值的发射测量;实际上,这表示谐波测量值应低于允许限值的90%。 注3:此外,对于I类测量仪器,各个通道间的相移需小于h×1°。 | |||
应对测量仪器测量频率范围之外的频率分量进行衰减处理,以免影响测量结果。为得到合适的衰 减,仪器可对输入信号以远高于测量范围的频率进行采样。例如,被分析信号可能会有超过25 kHz 的 分量,而仪器所考虑分量的最高频率却不超过2 kHz 。 这时应提供抗混叠低通滤波器,其-3dB 的截止 频点应高于测量范围,带外衰减应大于50 dB。
注:如,5阶巴特沃斯(Butterworth)滤波器在大约3倍于-3 dB频率处能得到50 dB的衰减。
在有必要评估额定电流大于5A 、15次以上的谐波,且要求不确定度最小时,建议使用外部分流器 或电流传感器,以便使测量范围与被测设备的额定电流相等。
对于仅仅用于谐波测量的仪器,仅对谐波分量有准确度要求。
为达到表1中规定的准确度,根据制造商给出的明确说明,可有必要通过内部或外部校准器对仪器 进行一些简单的调整。应规范校准器(如在内部)的不确定度。
制造商应标明仪器自身和内部校准器(如果提供的话)受主要影响因素(温度、辅助电源电压等)引 起的误差。
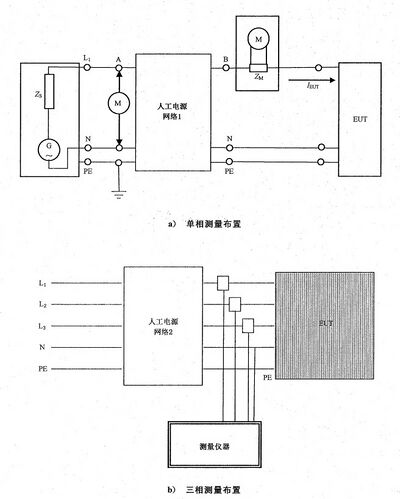
5.4 测 量 布 置 与 供 电 电 压
5.4.1 用 于 发 射 评 估 的 测 量 布 置
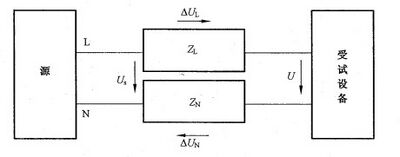
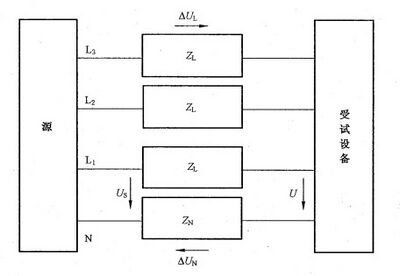
图 2 和 图 3 给 出 了 测 量 布 置 。
说明:
Us—— 相线—中性线间的电源电压;
U——EUT 端电压;
ZL,N—— 连接线和电流传感部件的阻抗; EUT—— 受试设备;
△U ——Z 和 ZN上的压降,△U=△UL+△UN;
L——相 线 ;
N——中 性 线 。
图 2 用 于 单 相 设 备 发 射 测 量 的 测 量 布 置
说明:
Us ——相线—中性线间的电源电压;
U ——EUT 端电压;
ZL,ZN—— 连接线和电流传感部件的阻抗; EUT ——受试设备;
△U——ZL和ZN上的压降,△U=△UL+△UN;
对于线与线之间的连接线,△U=2△UL;
L1-3 —— 相线;
N —— 中性线。
图 3 用 于 三 相 设 备 发 射 测 量 的 测 量 布 置
5.4.2 发射评估中使用的供电电压
5.4.2.1 概述
在对上限为40次谐波进行测量并对其进行评估时,在EUT 端的试验电压U 应满足以下要求。
5.4.2.2 每相输入电流小于或等于16 A 的设备要求
对于每相输入电流小于或等于16 A 的设备,应满足以下要求:
a) 试验期间,试验电压的稳定性应维持在所选定电压值±2%的范围之内,且频率应维持在所选 定频率值±0.5%的范围之内。若EUT 有指定的供电电压范围,则试验电压应与给设备供电 的电力系统的标称电压对应(例如,230 V 线一中性线间电压,与400 V 线一线间电压对应)。 如果电源是三线、三相三角形接线法,没有中性点,为便于测量,可采用三个匹配误差小于1% 的电阻来构成人工中性点。该中性点的目的是为了在采用线—中性线以及线一线的配置方案 下测量每相电压与功率。在发射试验期间,由仪器电压测量部分和任何安装的人工中性网络 负载效应引入的 EUT 电流测量误差不应超过0.05%。
注:很多情况下不需要人工中性点。但如需要,可采用如下方法。中性点可由测量仪器中三个电压测量输入阻抗 提供。作为一种选择,人工中性点也可由一个明显的网络加上仪器中电压测量回路输入阻抗的组合构成。人 工中性网络(如果存在)和电压测量回路的输入阻抗如此连接,可以避免电流测量时产生误差(由于加载发生在 电流互感器的源侧)。还有其他情况,由人工中性网络和测量仪器中电压测量回路输入阻抗的负载效应引起的 误差,可通过调整电源内的反馈回路进行适当补偿,消除这种测量引人的误差(否则会出现这种误差)。如果不 超过要求的不确定度,可接受多种其他的配置。
b) 对于三相电源供电情况,三个线电压应具有0°、120°±1.5°、240°±1.5°的相位关系。
c) 在 EUT 连接并运行在特定试验条件下时,EUT 的试验电压U 的电压谐波畸变不应超过以下数值:
——3次谐波,0.9%;
——5次谐波,0.4%;
——7次谐波,0.3%;
——9次谐波,0.2%;
——2~10次偶次谐波,0.2%;
——11~40次谐波,0.1%。
d) 试验电压的峰值应在其方均根值的1.404~1.424倍范围之间,且应在过零后87°~93°相位之 间到达峰值。
e) 在电流传感部件和连接线阻抗上的电压降△U 不应超过0.5 V(峰值电压)。
5.4.2.3 每相输入电流大于16 A 且小于或等于75 A 的设备要求
对于每相输入电流大于16 A 且小于或等于75A 的设备,应满足以下要求:
a) 输出电压U 应为设备的额定电压。若输出电压为一个范围,根据IEC 60038,输出电压应为标 称系统电压(例如:单相电压为120 V 或230 V, 三相线一线间电压为400 V) 。 如果电源是三 线、三相三角形接线法,没有中性点,为便于测量,可采用三个匹配误差小于1%的电阻来构成 人工中性点。该中性点的目的是为了在采用线—中性点以及线一线的配置方案下测量每相电 压与功率。在发射试验期间,由仪器电压测量部分和任何安装的人工中性网络负载效应引入 测量误差不应超过0.05%。
注:我国标准电压参见GB/T 156—2007。
b) 输出电压应维持在标称值的±2%,频率应维持在标称值的±0.5%范围之内。
c) 对于三相电源供电情况,电压不平衡度应低于IEC 61000-2-2 中所规定的不平衡电压兼容水 平的50%。
d) 空载条件下输出电压U 的谐波含有率不应超过:
——5次谐波,1.5%;
——3次与7次谐波,1.25%;
——11次谐波,0.7%;
——9次与13次谐波,0.6%;
——2~10次偶次谐波,0.4%;
——12次以及14~40次谐波,0.3%。
e) 为满足 IEC61000-3-12 中表2与表3,电源阻抗的短路比Rce (如IEC61000-3-12 中所述)应大 于或等于R 最 小 值(Rscemin),以便使设备满足符合性要求,可能的话串联一个电抗器。为满 足 IEC 61000-3-12中表4,电源阻抗的短路比 Rsc 应大于或等于最小值Ree 的1.6倍,以便使 设备满足符合性要求,可能的话串联一个电抗器。
注1:因子1.6考虑到如下因素:如果将设备连接至电源后,Rc 值大于Rscmm值,则谐波发射电流将增大。相关说 明见IEC 61000-3-12中表2与表3,此处不必补充说明。符合性测量依照Rsce是有必要的。
f) 电流互感器与连接线的阻抗包含在电源阻抗之内。
注2:考虑到高质量的大容量的电源极少,对上述阻抗值与畸变值进行了折衷。使用不同的电源,采用上述阻抗与 畸变值得出的测试结果的重复性可能较差。但采用相同电源时,测试结果的重复性较好。如果可能,可使用 畸变与阻抗值较低的电源。
5.4.3 设备的功率
若需要,应按照图2或图3的EUT 的端部电压U 和流入EUT 的电流来测量设备的功率。对于包 含有电流传感部件的电源,应通过电源输出端的电压和流入 EUT 的电流来测量设备的功率。在这种 情况下,如果电源在其输出端进行调节,则电压测量应选择在电流传感部件的 EUT 侧。
5.5 谐波发射的评估
以下内容与图1的后处理部分有关。
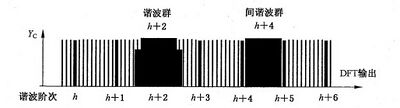
5.5.1 分群和平滑
为评估谐波,DFT 的输出“输出1”(见图1)首先根据式(8)进行分群,分群为两个邻近谐波之间的 各中间分量的平方和,如图4所示。仅使用2次谐波以上的中间分量。得到的第h 次谐波群(对应涂黑 区域的中心分量)具有幅值Yg,h (对于50 Hz 系统,该幅值等于整数倍谐波频谱分量的平方、紧邻的k= N×h-4 到 k=N×h+ 4 范围内各频谱分量平方与k=N×h-5 和 k=N×h+ 5 频谱分量平方一半 的和的平方根)。
[math]\displaystyle{ Y_{g,h}^2=\frac{1}{2}\cdot Y_{C,(N\times h)-N/2}^2+\sum_{k=(-N/2)+1}^{(N/2)-1}Y_{C,(N\times h)+k}^2+\frac{1}{2}\cdot Y_{C,(N\times h)+N/2}^2 }[/math]…………(8)
注:式中仅对2次谐波以上的中间分量进行计算。
式中:
Yc,(NXh)+k —— 与 DFT 输出值(频谱分量)对应的方均根值;
(N×h)+k—— 频谱分量的次数;
Yg,h —— 谐波群方均根值。
图 4 谐波群和间谐波群示意图(图示为50 Hz 电源)
注:图4中所示的间谐波群仅为明晰定义(间谐波电流评估参见附录 A)。
应对根据式(8)(图1中的“输出2a”)输出的各次谐波的方均根值Yg,h 进行信号的平滑处理。使用 一阶低通数字滤波器,其时间常数为1.5 s, 如图5所示。
[[文件:电磁兼容 试验和测量技术 供电系统及所连设备谐波、间谐波的测量和测量仪器导则GB 17626.7-2017_图5 数字低通滤波器的实现原理[z一'表示时间窗延迟,a、β为滤波器系数(数值见表 2)].jpeg|400px]]
图 5 数字低通滤波器的实现原理[z-¹ 表示时间窗延迟,α、β为滤波器系数(数值见表2)]
表 2 依据窗口宽度的平滑滤波器的系数
| 频率 | 时间窗内周期数N | 数字低通滤波器采样率 ms | α | β |
|---|---|---|---|---|
| 50 | 10 | ≈1/200 | 8.012 | 7.012 |
| 60 | 12 | ≈1/200 | 8.012 | 7.012 |
| 50 | 16 | ≈1/320 | 5.206 | 4.206 |
| 60 | 16 | ≈1/267 | 6.14 | 5.14 |
对于基波分量YH,1, 应对从“输出1”输出的方均根值YH,1 进行同样的平滑处理(若需要,例如对于 IEC61000-3-2 的 C 类以及可能的畸变系数)。
如果根据3.3,发射限值包含了通过谐波分量YH,A 导出的畸变因数THDy 或PWHDH,Y, 则应通过 “输出1”的值来计算。
如果根据3.3,发射限值包含了根据谐波分量 Yg,h 或 Ysg,h, 导出的畸变率 THDGy 、THDSY、 PWHDg,Y 或PWHDsg,Y, 则通过“输出2a” 的值来计算。
如果在相关标准中需要对上述畸变率进行平滑处理,应使用一阶低通数字滤波器,其时间常数为1.5 s,如图5所示,滤波器的相关系数见表2。
对有功功率P 和功率因数(若需要,例如IEC 61000-3-2对 C 类和D 类的要求),应对有功功率和功 率因数的模数进行相似的平滑处理 。
注:如果用来测量功率P 的时间分辨率约为200 ms, 则可使用外部功率表。因此可以预先在平滑模块前增加外部 功率表的输入,见图1。
为与谐波电压的调查相协调(见 IEC 61000-4-30),极力推荐一种更好的平滑方式:在根据式(8)计 算出的各谐波分量均方根值的基础上,其输出是对连续15个时间窗结果的平滑,每个时间窗(大约200 ms)或每15个时间窗(大约3 s)更新 一 次。
5.5.2 发射限值的符合性
应依照相关标准(例如 IEC 61000-3-2 、IEC 61000-3-6 、IEC61000-3-12 和 IEC 61000-4-30)中给定的条件,在进行数据的统计处理后再行评估发射是否符合限值。
5.6 电压谐波子群的评估
傅立叶变换分析假设信号是稳态的。然而,供电系统的电压幅值可能会出现波动,将谐波分量的能 量扩散到与之邻近频率的频谱上。为提高电压评估准确度,DFT 后每5 Hz 频率分量的输出 Uc,k, 应 根据图6和式(9)加以分群:
[math]\displaystyle{ Y_{sg,h}^{2}=\sum_{k=-1}^{1}Y_{\mathrm{C},(N\times h)+k}^{2} }[/math]…………………………(9)
式中,
Yc,(NXh)+k —— 与 DFT 输出值(频谱分量)对应的方均根值;
(N×h)+k—— 频谱分量的次数;
Ysg,h ——谐波子群的方均根值。
用符号I替代Y 则表示电流,单位为安培(A); 符 号U 代 替Y 则表示电压,单位为伏特(V)。
图 6 谐波子群和间谐波中心子群示例(图示为50 Hz 电 源 )
注:为进一步评估电压子群的平滑过程规定见 IEC61000-4-30。
6 其他分析原理
本部分指定DFT 仪器作为参考仪器的事实,并不排除应用其他分析原理,例如(数字)滤波器组或 诸如小波分析的其他分析原理。
此外,特殊条件下,为降低仪器成本,可以考虑采用较短时间窗或仅有一个周期的时间窗,但是这种 仪器不得用于评估非稳态信号是否符合发射限值,因为这类信号不能通过此方式进行评估。
根据其他分析原理的仪器规范,应注明各种影响因素引起的不确定度的范围,包括信号的非稳态特 性、混叠现象和信号同步故障等。不确定度应满足第5章的要求。
7 过渡期
推荐使用分群方法,尤其是对于波动性负荷。但在过渡期内,现存测量仪器如满足 IEC 61000-4-7: 1991 的要求,仍可继续使用。但是,使用这种仪器进行的测量,应在测试报告中标明“测量仪器依照 IEC 61000-4-7,1991"。
1) IEC 61000-4-7:1991,电磁兼容(EMC) 第4-7部分:试验和测量技术 供电系统及所连设备谐波、间谐波的测 量和测量仪器导则。
注:过渡期是必要的,因为在使用如5.5.1所述的分群方法之前,IEC 61000-3-2和IEC 61000-3-12的改变对一些设 备(例如那些使用对称多周期控制的设备)是必要的。
对于根据IEC 61000-4-71991使用16周期窗口进行的测量,平滑过程(图1中“输出2b”) 应根据表 2中的数据修正。且滤波器应按图5实施。
8 概述
制造商应明确说明额定工作条件和可能由下列变化引起的误差量级:
——温度;
——湿度;
——仪器供电电压和相关的串联干扰;
——仪器接地连接与其输入回路以及其他辅助供电电压之间的共模干扰电压;
——静电放电;
——辐射电磁场。
注:鉴于安全和绝缘要求而采用IEC 61010-1时,需考虑输入电路(电压和电流)可能会直接连接到供电电源的电 压 上 。
附 录 A
(资料性附录) 间谐波的测量
两个相邻的谐波频率之间含有频谱分量是因为信号中包含了间谐波分量。间谐波分量的来源主要 有两种:
——基波分量和/或谐波分量的幅值和/或相位角的变动,例如换流器驱动;
——电力电子回路的开关频率与供电频率不同步,例如交流/直流电源、功率因数校正器。
举例来说,可能的影响有:
——音频放大器的噪声;
——电动机和发电机的附加转矩;
——骚扰过零点检测,例如在调光器中;
——电感线圈中的附加噪声(磁致伸缩);
——纹波控制装置的阻塞或非正常运行。
测量布置应符合5.4的总体描述。
与间谐波分量有关的频谱分量不仅有幅值的变化,而且还有频率的变化。在两个连续的谐波分量 之间有一组频谱分量,从而构成一个间谐波群。这种组合给出了在两个离散的谐波分量之间所有间谐 波分量的综合值,也包含了谐波分量波动的影响。根据供电频率,可用式(A.1) 计算间谐波群的值:
[math]\displaystyle{ Y_{i_{g},h}^{2}=\sum_{k=1}^{N-1}Y_{C,(N\times h)+k}^{2} }[/math]…………………………(A.1)
注:式中下标ig,h 表示第h 次间谐波群(见图4和3.4.3)。本部分旨在将介于第h 次和第h+1 次谐波之间的间谐 波群的方均根值用Yig,h 来表示。例如,5次谐波和6次谐波之间的间谐波群表示为Yg,5。
从式(A.1) 中剔除紧邻谐波频率的分量,部分地减少了谐波幅值和相位角波动的影响。同样,为了 确定间谐波中心子群的方均根值Yg,h, 其分量,即图1中DFT 的“输出1”的输出数据,用式(A.2) 重新 组合(见3.4.4):
[math]\displaystyle{ Y_{isg,h}^{2}=\sum_{k=2}^{N-2}Y_{C,(N\times h)+k}^{2} }[/math]………………………(A.2)
该式中,Yc,(NXk)+k 是 由DFT 得到的频率超出第h 次谐波频率的相应频谱分量的方均根值,而 Yisg,h 则是第h 次间谐波中心子群的方均根值,例如,5次谐波和6次之间的间谐波中心子群表示为 Yisg,5,见图6和3.4.4。
注1:因为非稳态谐波会在谐波旁边生成旁带,与所考虑谐波直接相邻的频谱分量(k=1 和9或11)可能表征其幅 值和相位角的变化。所以,为给出间谐波中心子群,要把它们从间谐波群中剔除,参见图6。
注2:若仅对谐波进行评估,则可用分群式(8)。如果要分别评估谐波和间谐波(例如,评估设备是否产生间谐波), 则直接将某谐波相邻的频谱分量(k=-1 和+1)和该谐波一起组合成一个h 次谐波子群,而剩下的频谱分量 (k=2 至8或10)则按照式(A.2)构成一个第h 次的间谐波中心子群,参见图6。
间谐波群和间谐波中心子群的平滑方式与谐波测量相同,参见5.5.1。不建议只对间谐波分量进行 平滑处理。
注:IEC 61000-4-30已经给出进一步的平滑过程。
对间谐波的准确度要求与谐波测量相同,参见表1。
附 录 B
(资料性附录)
谐波频率范围以上至9 kHz 的测量
B.1 概述
信号(电流或电压)中高于40次谐波频率(约2 kHz) 且又低于低频范围上限(9 kHz) 的分量是由于 诸如此类的现象而产生的:
——连在电源侧的电源脉宽调制控制(与主电源频率同步或异步),例如用于(有源)功率因数校正 系统;
——发射,诸如电源的信令;
——通过电源变换器负载侧或发电机侧对电源系统侧的反馈分量;
——由换相缺口引起的振荡。
这些分量可以是单一频率的,也可以是宽频带的。
这些分量的测量在频域不需要很高的分辨率。而习惯上是将要分析的信号能量聚集到预定的频 带中。
对于频率分析,推荐使用第4章所述的DFT 方法。
此目的之一是对2 kHz~9kHz 范围内的信号进行发射分析,通常采用小幅值、合适的网络阻抗 (见图B.3) 来滤除起主导作用的低次谐波。在使用滤波器后,2 kHz~9 kHz 范围内的 EUT 测试电压 可直接来自低压网络,但要求电压稳定、在合适频率下满足容差要求。如不能从公共低压网络获取合适 频率或电压时,可使用适当的电源。
另外,如测量仪器内部有滤波器组合和足够大的动态测量范围,即使不使用上述滤波器也可分析 2 kHz~9 kHz频率范围内的信号。
B.2 基本仪器
这种较高频率范围的测量,可按4.4.1进行离散傅立叶变换,且按照本附录进行改造。
外部电压和电流传感器的频率范围应适用2 kHz~9 kHz的测量。
由于要测量的信号较弱,可用带通滤波器抑制基波和9 kHz 频率以上的分量幅值,从而大大减少 测量的不确定度。对基波频率的衰减要超过560倍(55 dB)。
注1:与基波电流、电压的幅值相比,待测分量幅值在2×10-⁵~5×10-2范围内。
采样频率应按已有的信号分析的既定规定选取,使频率高达9 kHz 的分量都能测到。可采用宽度 为200 ms 的矩形数据采集窗,约相当于50 Hz(60 Hz)系统的10(12)个周期。这样,两个连续的被测分 量 Yc,f之间的频率差是5 Hz。
注2:采样频率无需与电源频率同步。
频率为f 的分量的方均根值为Yc,f, 例如Yc,3 160是频率3160 Hz 分量的方均根值。
电流与电压输入电路应分别满足5.1与5.2的要求。
B.3 分群
DFT 的原始输出(图1中的“输出1”)应按200 Hz 的带宽分群(见图 B.1), 起点在高于谐波范围之上的第1个中心带宽。第1个群的中心频率对于50 Hz 以及60 Hz 系统分别为2.1kHz 和2.5 kHz。 每个频带的输出YB,b是方均根值,见式(B.1):
[math]\displaystyle{ Y_{B,b}=\sqrt{\sum_{f=b-95\mathrm{Hz}}^{b+100\mathrm{Hz}}Y_{\mathrm{C},f}^{2}} }[/math]…………………………(B.1)
式中:
YB,b——每个频带的输出的方均根值;
Yc,f——频率为f 的分量的方均根值。
用符号 I 替代Y 则表示电流,单位为安培(A); 符号U 代替Y 则表示电压,单位为伏特(V)
注1:选取200 Hz频带分群是为了与CISPR 16-1-2中对9kHz以上的信号带宽处理相一致。
注2:中心频率b 如2100 Hz 、2300 Hz 、2500 Hz等频率代表了该段频带。最高的中心频率为8900 Hz,见图B.1。
注3:对于60 Hz电力系统,谐波范围以上的分量频率大于2400 Hz。
注4:当谐波范围以50次谐波结尾时,式(B.1)对于6>2500的50Hz电力系统以及6>3100的60Hz电力系统均适用。
图 B.1 50Hz电力系统中40次谐波频率以上至9 kHz 的频带范围内测量示意图
B.4 发射评估用的测量布置
为了提高发射评估测量结果的可重复性,需要明确定义电源侧的阻抗。因此应在电源端以及 EUT 端之间插入人工电源网络(AMN), 以使电源侧在2 kHz~9kHz 范围内的阻抗特性标准化,测量布置 见图 B.2。
注:CISPR 16-1-2中的方法适用于9 kHz以下频率。
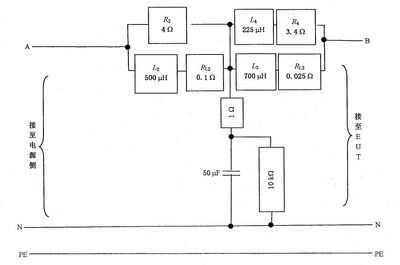
AMN 内部电路(用于单相时)如图B.3 所示。
发射测量时,需要测量 AMN 与 EUT 之间导线上的电流,如图 B.3 中的B 点。
图 B.2 通 用 的 测 量 布 置
网络2是由3个网络1单元组成,并将所有的中性点连接在一起。
图 B.3 适用于16 A 电流及以下测量的人工电源网络
注:如果使用交流电源,其电感与电阻分别不可超过160 μH 和0.1Ω。
B.5 性能要求
用单频率信号进行测量时,总体测量不确定度(测试仪器包括分流器或 CT) 不得超过被测电流的 ±10%。仪器制造商应明确说明该±10%的不确定度所适用的测量范围。
包括AMN 在内总体测量不确定度不应超过所适用群值YB,b的±15%。
注:电源需满足 EUT 的工作需要。如果提供了合适的频率、电压以及足够可用的额定功率,低压供电系统可作为
测试电压源。也可采用其他合适的电源。
如果在B 点使用电流分流器,其电阻最高为0.02Ω。
当 A 直接连至 N 时,在 B 和 N 之间测量,AMN 应提供给 EUT 的阻抗特性,应在图 B.4 所示 2 kHz~9 kHz特性的±5%范围内。因此需要选择元件的容差,以使得在 EUT 电流、温度、频率在运 行条件之内时,阻抗特性不超过其容差范围。记住要根据该容差设计AMN 的物理布局、封装以及温度控制措施。
图 B.4 从 EUT 侧 看 人 工 电 源 网 络 阻 抗
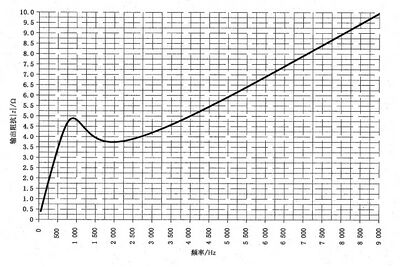
在2050 Hz 以及2450 Hz, 输出阻抗分别为3.745051以及3.868689Ω。频率f 大于3kHz 时的 输出阻抗由式(B.2) 计算:
[math]\displaystyle{ \mid z\mid=\sqrt{8.819+1.23\times10^{-7}\times f^2\ln(f)} }[/math] …………………………(B.2)
式 中 :
|z|—— 输出阻抗,单位为欧姆(Q);
f ——频率,单位为赫兹(Hz)。
附 录 C
(资料性附录)
分群方法所考虑的技术性因素
经仔细考虑并平衡各种竞争目标(例如,测量带宽与频率分辨率),得到本部分所定义的测量方法。 某些情况下,需要确定一种切实可行的测量方法,来折衷表征所研究的信号特性,并非获得最高的精度。 本附录详细描述了处理几个难点问题的考虑。
注:在本部分中,除非另有说明,电压、电流的值均用方均根值表示。
C.1 时域信号表征和频域信号表征的功率等值
帕斯瓦尔(Parseval) 关系式,也称为瑞利(Rayleigh) 能量定理,定义信号功率(或能量)在时域和频 域中的等价关系,见式(C.1):
[math]\displaystyle{ \int_{-\infty}^{+\infty}\left[g\left(t\right)\right]^{2}\mathrm{d}t=\frac{1}{2\pi}\int_{-\infty}^{+\infty}\left|G\left(\mathrm{j}\omega\right)\right|^{2}\mathrm{d}\omega }[/math]…………………………(C.1)
式中:
g(t)— 时域函数;
G(jw)—— 时域函数的傅立叶复变换,w=2πf。
注:由于功率与电压或电流的平方成正比,因此,信号的平方被看作信号的“功率”。例如,如果设g(t)是某电压的 时域函数,则公式左侧(时域)的物理量纲应该是 V²s (能量)。傅立叶变换表示的是电压的频谱密度,在上例 中,G(jw)的量纲就是 V/Hz 或者Vs, 即该公式右侧的量纲也是 V²s(能量)。
如果为非周期函数,则其频谱是连续的。但是,如果是周期函数,则它可以用在时间窗 T 内表征, 即用该时间窗的无限重复可生成整个函数g(t) 。 该时间受限信号的傅立叶变换就不再连续,而是由按 fw=1/T 频率分隔的频谱分量构成。时间窗 T 和在频率f=k×fw 的频谱分量(复数)方均根值平方G 的积,近似表示从f-fw/2 到 f+fw/2 积分的连续频谱密度的“能量”。由所有频谱分量贡献的 “能量”总和就等值于在时间窗内该时域函数的“能量”。将该“能量”除以时间窗的时间 T。就 得 到 式(C.2):
[math]\displaystyle{ \frac{1}{T_{w}}\int_{-T_{w}/2}^{+T_{w}/2}\left[g\left(t\right)\right]^{2}\mathrm{d}t=\sum_{k--\infty}^{\infty}\left|G_{k}\right|^{2} }[/math]…………………………(C.2)
式中,左边相当于时间函数在时间窗内的平均“功率”,右边对应于频域内所有频谱分量的总“功 率”。
傅立叶变换的一个性质,是在负数频率的频谱分量是在同一正数频率频谱分量的共轭复数,即“功 率”频谱关于频率f=0 是对称的。将频谱的负数部分取正,与正数部分叠加,则式(C.2) 可简化为 式(C.3):
[math]\displaystyle{ \frac{1}{T_{w}}\int_{-T_{w}/2}^{+T_{w}/2}\left[g\left(t\right)\right]^{2}\mathrm{d}t=G_{0}^{2}+2\sum_{k=1}^{\infty}\mid G_{k}\mid^{2} }[/math]…………………………(C.3)
按照本部分中式(3)的傅立叶分量的幅值ck, 其定义与 Tw/2 而 不 是 Tw有 关(c。除外,与 Tw 有 关),即ck=2×G 或 Ck=√2×Gk 。 因此,式(C.3) 可改写成式(C.4):
[math]\displaystyle{ \frac{1}{T_{w}}\int_{-T_{w}/2}^{+T_{w}/2}\left[g\left(t\right)\right]^{2}\mathrm{d}t=c_{0}^{2}+\sum_{k=1}^{\infty}\mid C_{k}\mid^{2}=\sum_{k=0}^{\infty}\mid C_{k}\mid^{2} }[/math]………………(C.4)
实际上,求和式中系数的个数应限制:k=1,…K 。 如果对于频率fk≤K×fw 有限带宽信号,下标k>K 的系数则没有“功率”,在式(C.4) 的求和式里可不考虑这些系数。但该频率fk 应远超过仪器的 工作频率范围 。
C.2 数字化实现的特性
本部分考虑了数字仪表。为了满足香农定理,应该以f,>2×f 的采样频率对时域信号进行采样, 所以,原则上可以计算出一直到C 的所有系数。一个时间窗内的采样点数为N=f,×Tm。
在上述的理想条件下,即数字化的信号是周期性、有限带宽的实数,且时间窗与信号周期同步,
式(C.4) 可改写成式(C.5):
式 中 :
[math]\displaystyle{ \sqrt{\frac{1}{N}\sum_{i=1}^{N}\left[g\left(t_{i}\right)\right]^{2}}=\sqrt{\sum_{k=0}^{N/2}\mid C_{k}\mid^{2}} }[/math]…………………………(C.5)
g(ti)—— 时域函数在采样点的值;ti=i×Tw/N 。 式(C.5) 表明,信号通过采样和数字化,其频域 分量的方均根值等于它在时域中的方均根值。在某些特定的情况下,可利用帕斯瓦尔关 系式来确定功率频谱是否能准确地描述时域信号。
在上述设定的理想条件下,由本部分给定方法计算出的功率频谱是被测信号在指定的时间窗内各 频谱分量的平均功率。这种功率频谱准确地反映了被测信号的总功率、各单一频率分量的功率及其频 率。在实际情况下,当被测信号的所有分量确实是“基础”频率fw=1/T 的谐波时,这种理想的条件才 存在。由于本部分对同步有严格的要求,这种近于理想的条件仅在电力系统的基波频率和其他频率分 量为基础频率的整数倍时才出现,当然,也包括了信号分量为基波频率的谐波的情况。
注:“基础”频率是时间窗宽度的倒数,“基波”频率是电源系统周期的倒数。
按照IEC61000-4-7 的第1版本的要求,当时的测量仪器设计中,时间窗的宽度是按16个周波来确 定的(≈320 ms 或≈267 ms) 。 将来设计测量仪器时,时间窗的宽度 Tw≈200 ms,是按系统频率为 50 Hz或60 Hz 时分别取10或12个周波来确定的。因此,频谱分量间的频率间隔(基础频率fw) 分别 ≈5 Hz 、≈3.125 Hz或≈3.75 Hz 。根据本部分的式(8)所给出的分群方法能确保准确地计算信号的总 功率。它不仅包括基波频率整数倍的(谐波)分量,而且考虑到了所有的频谱分量。式(8)是仅按频谱分 量间的频率间隔≈5 Hz 给出的,因此,当采用其他“基础”频率时,该公式要作修改。在理想条件下,帕 斯瓦尔关系式描述的功率频谱就可以准确地反映被测信号的平均功率,必要时应作上述修正。
在不太理想的情况下,如信号含有频率为 f≠k×fw(k 是整数)的非谐波信号的成分,由于频率泄 漏现象引起频率信息损失,但信号功率通常能准确地描述。对于时间窗等于200 ms 的情况而言,只要 存在不是5 Hz 整数倍频率的间谐波信号(如287 Hz), 或者在分析的时间窗内信号幅值有波动,就会出 现非谐波的信号成分。本部分给出的分群方法有助于确保在大部分情况下能准确评估总功率。至于功 率如何分配到某个特定的信号组,那就取决于被测信号的特性了。
以下几个示例会有助于说明这一点。C.3 中的示例说明了电压、电流信号幅值波动的影响。C.4 中 说明了间谐波的影响。为了在图中以全屏的尺寸更加清楚地显示频谱线和分群的作用,在电压、电流信 号中实际上占有主导地位的基波分量被省略了。
C.3 谐 波 的 波 动
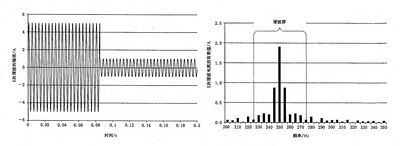
示例1:
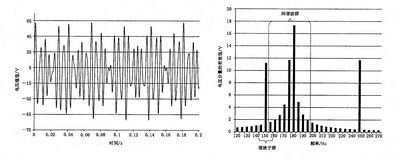
图 C.1 表示的是5次谐波电流方均根值从3.536 A 波动至0.7071A 的例子。电流的阶跃是在21.25个5次谐波周 期之后出现的。对于这个例子,预期的电流方均根计算值应是2.367 A。但测得的5次谐波(单一频谱)结果仅为1.909 A, 即忽略了其他频谱分量产生了19.3%的误差。在这个例子中,谐波子群的测量值为2.276 A, 其误差已减少到3.84%,但谐波群的测量值为2.332 A, 相应的误差小至仅为1.47%。
图 C.1 5 次谐波电流大波动
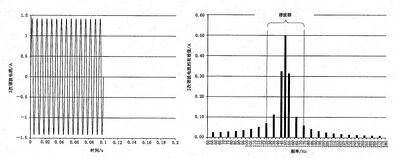
示例2:
电力系统的谐波电压通常是由几个非线性负载产生的谐波电流共同注入造成的结果。这些负载通常不会明显关联 地波动。此外,系统中还有准稳定的负载。所以,谐波电压高振幅、快速波动的情况是一种例外,在电力系统中很少出 现。例如,图C.2 表示5次谐波电压的方均根值由13.225 V 减少到9.775V 的情况。在这个例子中,总的方均根期望值 应是11.37 V, 但是单一谐波频谱分量仅为11.24 V。用本部分推荐的算法得到谐波子群值11.33 V, 以及谐波群值 11.34 V,对应的误差仅分别为0.35%和0.24%,远低于测量仪器本身的不确定度。
图 C.2 5 次谐波电压大波动
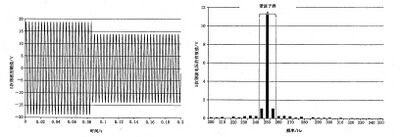
示例3:
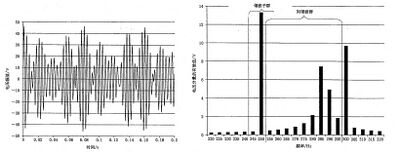
某连续运行的微波器具会产生(含有)3次谐波电流,例如1A, 它的平均功率由多周期过零的方法控制(例如,按 5 Hz的速率重复,占空系数为50%)。图 C.3 表示了3次谐波电流的时间函数及其相应的频谱。总的电流方均根值应 为0.707 A 。3次谐波频谱分量的方均根值为0.5 A, 相应的误差为29.3%。由谐波子群得到的值为0.673 A, 误差仅为 4.8%,而由谐波群得到的值为0.692 A, 误差也减少到了2.0%。
图 C.3 某微波器具波动的3次谐波电流
这些示例证明通过分群步骤给出的结果较好地满足帕斯瓦尔公式。
C.4 间谐波
示例1:
通信(信号传输)系统也会加载在电力系统上。为了避免受到谐波的干扰,它们所采用的频率通常介于两个谐波频 率之间,即间谐波频率。如果它们的频率是“基本频率”f 的整数倍,并在时间窗内又有恒定的幅值,那么,频谱只是在 该频率上显示一条附加的频谱分量,而并不一定需要额外的分群。但是,为了传递信息,信号需要调制。这时对频谱的 影响与前面几个示例相似,仅有的差异只是从调制信号得到的频谱分量是以信号传输频率为中心的一组频谱分量。按 附录A 介绍的“间谐波群”的方法,可以按 C.3 中谐波分群方法减少误差。
在许多情况下,传输使用的信号都不是fw整数倍的频率。例如,图C.4 显示一个方均根值保持为23 V、频率为178 Hz 的通信信号迭加在系统中本已存在的3次和5次谐波(幅值均为11.5 V) 之上。尽管离散傅立叶变换不能直接分解出 178 Hz的功率,它却能把功率分散到该频率的临近的频谱分量上(所谓的“泄漏”)。这时,3、5次谐波之间的间谐波组 (参见附录A)收集了该通信信号分散功率的主要部分,得到的值为22.51 V,误差只有2.15%。
图 C.4 178 Hz 的通信信号以及3次、5次谐波
注1:对于频率为非“基本频率”整数倍的信号来说,其“泄漏”效应就是在原有的谐波矢量上添加了一个附加矢量 (见图C.7) 。 同一频率的附加矢量与原始谐波矢量之间的相位角在各个时间窗中的增加(或减少)几乎相等。 合成矢量的大小则根据实际相位角的不同在这两个矢量差及矢量和的幅值之间变化。在所给的示例中,原始 谐波矢量的大小为11.5 V,150 Hz时≈1.2 V、250 Hz时≈0.4 V (见图 C.4),则合成矢量的大小对于150 Hz 在≈10.3 V 和≈12.7V 之间变化,对于250 Hz 在≈11.1V 和≈11.9 V 之间变化。由许多个毗邻时间窗得到 的合成矢量的方均根值等于原始谐波矢量与附加矢量共同的方均根值,该例中150 Hz 时11.56 V 、250 Hz 时11.51V 。 分群之后的平滑过程使结果的变化大大减少,并给出了一个接近于共同的方均根值的平均输出量。 注2:实际上,通信信号的幅值比本例中所述的要小,所以,它的“泄漏”效应将相应地减小。
示例2:
在发射电流的方均根值中也会有间谐波,并因此也会出现在电源电压的方均根值中。它们会随机地出现在两个毗 邻的谐波之间。例如,图C.5 给出了频率为287 Hz、幅值为9.8V 的间谐波以及13.2V 的5次谐波和10V 的6次谐波。 从频谱中可以看出其“泄漏”效应。从5次间谐波群(见3.4)得到的值为9.534 V, 其误差为2.7%。
图 C.5 287 Hz 的 间 谐 波 以 及 5 次 和 6 次 谐 波
示例3:
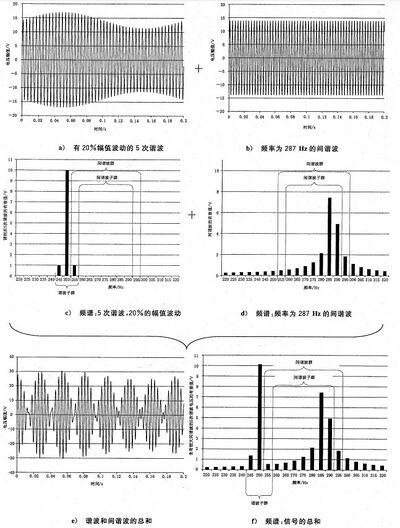
如图 C.6a)所示, 一个变转矩的电子式马达驱动(例如活塞泵)会在供电系统中产生5次谐波,其幅值有5 Hz、20% 的正弦调制,围绕平均方均根值10V 波动。时域函数在0.2 s 时间内的总方均根值评估为10.10 V 。其频谱中的250 Hz 频率含有一根方均根值为10 V 的“载波”分量,并在两侧频率245 Hz 和255 Hz 各有 一 根1 V 分量,见图C.6c)。250 Hz 处单根频谱分量的误差为0.99%;而由谐波子群得到的结果就没有误差了。
在同一个系统中可加载频率为287 Hz、幅值为9.8 V 的通信信号[见图C.6b|400px]]。 该信号在以200 ms 时间窗内的周 期数为57.4次,是非整数,从而在频谱中出现“泄漏”效应(见图 C.6d)] 。 由间谐波群得到的方均根值为9.538 V, 误差为 2.7%。
当波动的谐波和通信信号同时加载在电压上时[见图 C.6e|400px]], 总的方均根值为14.07 V 。所得到的频谱分量可用不 同的组合方式加以组合[见图C.6f|400px]] 。 因为在250 Hz 存在谐波,而且从频谱的包络线来看在285 Hz 附近有明显的信 号,用两个群的方式就合理一些(但每个频谱分量只能用一次):
——9.36V 的间谐波群(相对于9.8 V 的误差为4.5%)和一根10. 16 V 的谐波频谱分量(相对于10.0 V 的误差为 1.6%),结果是总的方均根值为13.81 V (相对于14.07 V 的误差为1.8%);
——9.34 V的间谐波子群(相对于9.8V 的误差为4.7%)和10.23 V 的谐波子群(相对于10.1V 的误差为1.29%),
结果得到总的方均根值为13.85 V(相对于14.07 V 的误差为1.5%)。
第2种组合方式更符合“物理意义”,因为245 Hz 和255 Hz 的频谱分量并不在“泄漏”的包络线之中。如果注意观 察几个毗邻的时间窗的频谱的话,这一点就很清楚了。
图 C.6 调制后的5次谐波和频率为287 Hz 的 间 谐 波
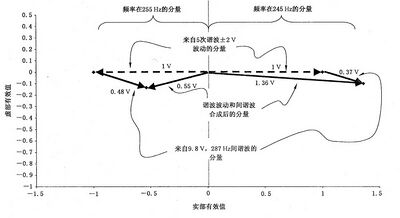
5次谐波两侧旁带得到的频谱分量主要是泄漏效应的结果。对于一个波动的谐波来说,谐波旁带频率(即245 Hz 和255 Hz) 分量的矢量,其大小相等,方向相反。矢量的大小在恒定的调制深度下保持不变。但是,如果调制频率不是 基本频率的整数倍,其角度从一个时间窗到下一个时间窗会一步一步地旋转。由频率为287 Hz 的间谐波得到的矢量的 大小也几乎保持不变,但因为该间谐波在时间窗中的位置在改变,所以对各个时间窗来说该间谐波矢量的角度在改变。 当然,由调制和泄漏合成的矢量,其大小和角度在不同的时间窗内也在改变。图C.7 表 示 的 是 图 C.6 所示的时间窗内 5次谐波上下各5 Hz 的分量。这时,相对于“调制”矢量来说,245 Hz 的合成幅值是增加了,而255 Hz 的合成幅值是减 小了。在其他的时间窗内由287 Hz 的信号产生的矢量就有其他的角度,相应的合成矢量的幅值也就不同。频谱的时间 表示方式在245 Hz 和255 Hz 处显示出频谱分量的波动,而该时间段的平均值却近似于“调制”和“泄漏”矢量的共同的 方均根值。
图 C.7 频 率 分 别 为 2 4 5 Hz 和 2 5 5 Hz 处 的 矢 量
参 考 文 献
[1] GB/T 156—2007 标准电压
[2]IEC 61000-3(all parts),Electromagnetic compatibility(EMC)-Part 3:Limits
[3] IEC 61000-3-4:1998,Electromagnetic compatibility(EMC)-Part 3-4:Limits—Limitation of emission of harmonic currents in low-voltage power supply systems for equipment with rated cur- rent greater than 16A
[4] IEC 61000-4-30,Electromagnetic compatibility(EMC)-Part 4-30:Testing and measurement techniques—Power quality measurement methods
[5] IEC 61010-1:2001,Safety requirements for electrical equipment for measurement,control, and laboratory use—Part 1:General requirements
[6] CISPR 16-1:1999,Specification for radio disturbance and immunity measuring apparatus and methods—Part 1:Radio disturbance and immunity measuring apparatus