电磁兼容 试验和测量技术 静电放电抗扰度试验GB 17626.2-2018:修订间差异
无编辑摘要 标签:移动版编辑 移动版网页编辑 |
无编辑摘要 |
||
| 第1,424行: | 第1,424行: | ||
——A 类:用统计的方法评定,估算一系列的试验标准差。它们通常服从正态或高斯分布。 | ——A 类:用统计的方法评定,估算一系列的试验标准差。它们通常服从正态或高斯分布。 | ||
{| class="wikitable" | |||
|- | |||
! 分布 | |||
! 合成不确定度 | |||
! 备注 | |||
|- | |||
| 正态或高斯 | |||
| <math>U_{\mathrm{C}}(y)=\sqrt{\frac{1}{(n-1)}\sum_{j=1}^{n}(u_{j}-\overline{u})^{2}}</math> | |||
| 通常来自验证记录 | |||
|} | |||
——B 类:由其他方法评定。它们通常与失 配 、电缆损耗以及仪器非线性特性相关。可以基于校准 数据,仪器制造商的规范或简单的通过知识和经验在分析中评估 B 类不确定度的大小和 分 布 。 | ——B 类:由其他方法评定。它们通常与失 配 、电缆损耗以及仪器非线性特性相关。可以基于校准 数据,仪器制造商的规范或简单的通过知识和经验在分析中评估 B 类不确定度的大小和 分 布 。 | ||
| 第1,556行: | 第1,565行: | ||
如静电放电枪的方向等方面可认为是A 类的不确定度,而且在本部分中一般不涉及到这些不确定 度。一个例外就是已经考虑的测量和校准测量系统的重复性。 | 如静电放电枪的方向等方面可认为是A 类的不确定度,而且在本部分中一般不涉及到这些不确定 度。一个例外就是已经考虑的测量和校准测量系统的重复性。 | ||
E.7 校准结果的不确定度 | E.7 校准结果的不确定度 | ||
| 第1,567行: | 第1,574行: | ||
表 E.1 静电放电上升时间校准的不确定度报告实例 | 表 E.1 静电放电上升时间校准的不确定度报告实例 | ||
{| class="wikitable" | {| class="wikitable" | ||
|- | |||
! 因素 | |||
! 分布 | |||
! 值 ps | |||
! ui(y) ps | |||
! ui(y)² ps² | |||
! 备注 | |||
|- | |- | ||
| 峰值读数 | |||
| 正态k=2 | |||
| 50 | |||
| 25 | |||
| 625 | |||
| 峰值6.3%不确定度 (表E.2)乘以测得的上升时间800 ps | |||
|- | |- | ||
| | | 90%峰值电流的时间读数 | ||
| 矩形因子=√3 | |||
| 25 | |||
| 14 | |||
| 196 | |||
| 示波器采样率20 GS/s | |||
|- | |- | ||
| | | 10%峰值电流的时间读数 | ||
| 矩形因子=√3 | |||
| 25 | |||
| 14 | |||
| 196 | |||
| 示波器采样率20 GS/s | |||
|- | |- | ||
| | | 总示波器水平测量因素(注1) | ||
| 正态k=2 | |||
| 36 | |||
| 18 | |||
| 324 | |||
| 来源于示波器的校准试验室 | |||
|- | |- | ||
| | | 靶-衰减器-电缆链 | ||
| 正态k=2 | |||
| 30 | |||
| 15 | |||
| 225 | |||
| 来源于示波器的校准试验室(注2) | |||
|- | |- | ||
| | | 重复性 | ||
| 正态因子=1 | |||
| 45 | |||
| 45 | |||
| 2025 | |||
| 由A类评估获得(注3) | |||
|- | |- | ||
| | | | ||
| | |||
| | |||
| 总计 | |||
| 3591 | |||
| | |||
|- | |- | ||
| || || | | | 上升时间的合成标准不确定度ue | ||
| | |||
| | |||
| 根 | |||
| 60 ps | |||
| | |||
|- | |- | ||
| | | 上升时间的扩展不确定度U | ||
| 正态k=2 | |||
| 120 ps (15%) | |||
| | |||
| | |||
| 置信度95% | |||
|- | |- | ||
| | | colspan="6" | 注1: 总示波器水平测量值因素包括示波器水平分辨率,插值分辨率,时基分辨率,频率测量,上升时间修正等不确定度因素。<br /> <br />注2: 链的校准证书通常只包括衰减的频率响应。在此假设,上升时间测量的不确定度分量也由校准试验室提供,因此k=2。<br /> <br />注3: 重复性需要至少5次的连续测量。这是A类评估,由n次重复测量得到标准差s(可)的公式为:<br /><br /><math>s\left(\overline{q}\right)=\sqrt{\frac{1}{n\left(n-1\right)}\sum_{j=1}^{n}\left(q_{j}-\overline{q}\right)^{2}}</math><br /><br />其中q<sub>j</sub>:第j次的测量结果;<math>\overline{q}</math>:结果的算术平均值。 | ||
|} | |} | ||
表 E.2 静电放电峰值电流校准的不确定度报告实例 | 表 E.2 静电放电峰值电流校准的不确定度报告实例 | ||
{| class="wikitable | {| class="wikitable" | ||
|- | |- | ||
! 分量 | ! 分量 | ||
! 分布 | ! 分布 | ||
! 值 % | ! 值 % | ||
! | ! ui(y) % | ||
! | ! ui(y)² %² | ||
! 备注 | ! 备注 | ||
|- | |- | ||
| 总示波器垂直测量 分量(注1) | | 总示波器垂直测量 分量(注1) | ||
| 正态k=2 | | 正态k=2 | ||
| 第1,634行: | 第1,675行: | ||
| 3.24 | | 3.24 | ||
| 来自校准实验室 | | 来自校准实验室 | ||
|- | |- | ||
| 示波器链的不匹配 | | 示波器链的不匹配 | ||
| U形 因子= √ 2 | | U形 因子= √ 2 | ||
| 第1,648行: | 第1,689行: | ||
| 9×10<sup>-12</sup> | | 9×10<sup>-12</sup> | ||
| 内部校准(注3) | | 内部校准(注3) | ||
|- | |- | ||
| 重复性 | | 重复性 | ||
| 因子=1 | | 因子=1 | ||
| 第1,662行: | 第1,703行: | ||
| 10.05 | | 10.05 | ||
| | | | ||
|- | |- | ||
| 峰值电流的合成标 | | 峰值电流的合成标 准不确定度uc | ||
| | | | ||
| | | | ||
| 第1,676行: | 第1,717行: | ||
| | | | ||
| 置信度95% | | 置信度95% | ||
|- | |||
| colspan="6" | 注 1:总示波器垂直测量分量包括示波器垂直分辨率、低频线性度、高频线性度、偏置分辨率等。校准需要覆盖全频段,即 f ≤ 2 GHz。然而,在截止频率为 f<sub>c</sub> = 2 GHz 的一阶滤波器下,平坦度不必更好,即 <math>A(f)\sim\mid1+(f/f_{\mathrm{c}})^2\mid^{-1/2}</math>。<br /><br />注 2:失配分量是由轭-衰减器-电缆链的输出反射系数 Γ<sub>c</sub> 和示波器的输入反射系数 Γ<sub>0</sub> 来决定的。他们宜从校准证书或技术规范上获得。由于 Γ 中二阶分量的误差,一个可靠的技术规范就够了。但是请注意,技术规范也要覆盖全频段,示波器通常不是这样,所以需要额外的测量。<br /><br />失配分量:Γ<sub>c</sub>× Γ<sub>0</sub>,U 型分布,因此除数为 √2。<br /><br />这个失配不确定度的公式假设了示波器的幅度响应已根据射频校准的概念进行了校准,即电压误差是基于 50Ω 源的人射电压而不是输入的实际电压。这宜在证书上核实,否则需应用不同的公式。<br /><br />注 3:这里假定试验室有一个单独的校准指导书,其不确定度的评估得到此校准的扩展不确定度 U。<br /><br />注 4:至少取得连续 5 次的测量值来得到重复性。这是 A 类评估,由 n 次重复测量值得到标准差 <math>s\left(\overline{q}\right)</math>的公式为:<br /><br /><math>s(\overline{q})=\sqrt{\frac{1}{n(n-1)}\sum_{j=1}^{n}(q_{j}-\overline{q})^{2}}</math><br /><br />其中 q<sub>j</sub>,第 j 次的测量结果;<math>\overline{q}</math>,结果的算术平均值。 | |||
|} | |} | ||
表 E.3 静电放电中I ₃0,I 6o校准不确定度评估实例 | 表 E.3 静电放电中I ₃0,I 6o校准不确定度评估实例 | ||
2025年7月1日 (二) 11:03的最新版本
引用资料
文件:电磁兼容 试验和测量技术 静电放电抗扰度试验GB 17626.2-2018.pdf
标准状态
当前标准:电磁兼容 试验和测量技术 静电放电抗扰度试验GB 17626.2-2018
发布日期:2018-06-07
实施日期:2019-01-01
旧标准:电磁兼容 试验和测量技术 静电放电抗扰度试验GB/T 17626.2-2006
发布日期:2006-12-19
实施日期:2007-09-01
废止日期:2019-01-01
1 范围
GB/T 17626 的本部分规定了电气和电子设备遭受直接来自操作者及其操作者对邻近物体的静电 放电时的抗扰度要求和试验方法,还规定了不同 环境和安装条件下试验等级的范围和试验程序。
本部分的目的在于建立通用的和可重现的基准,以评估电气和电子设备遭受静电放电时的性能。此外,它还包括从人体到靠近关键设备的 物体之间可能发生的静电 放 电。
本部分的规定包括:
——放电电流的典型波形;
—— 试验等级的范围 :
—— 试验设备;
—— 试 验配置 ;
—— 试 验程序 ;
—— 校准程序;
——测量不确定度。
本部分对“实验室”试验和“设备安装完成 试验”提 技术要求。
本部分不对特殊设备和系统的试验进行规定其主要日的是为所有有关专业标准化技术委员会提 供一个通用的基本准则。有关专业标准化技术委员会(或设备的使用者和制造者)负责选择试验和确定 试验条件的严酷 等 级。
为了不妨碍协调和标准化的任务,极力建议有关专亚标准化技术委员会或用户和制遣商考虑(在其未来的工作或原标准的修改中)采用本部分中规定的相关抗扰度试验。
2 规范性引用文件
下列文件对于本文件的应用是必不可少的。凡是注日期的引用文件,仅注日期的版本适用于本文 件。凡是不注日期的引用文件,其最新版本(包括所有的修改单)适用于本文件。
GB/T4365—2003 电工术语 电磁兼容[IEC60050(161):1990,IDT]
IEC 60068-1 环境试验 第1部分:总则和指南(Environmental testing—Part 1:General and guidance)
3 术语和定义
GB/T 4365—2003 界定的以及下列术语和定义适用于本文件。为了便于使用,以下重复列出了 GB/T4365—2003 中的一些术语和定义。
3.1
空气放电方法 air discharge method
将试验发生器的充电电极靠近受试设备直至接触到受试设备的一种试验方法。
3.2
抗静电材料 antistatic material
在同种材料或与其他类似材料相互摩擦或分离时,具有产生电荷量最小特性的材料。
3.3
校准 calibration
参照标准,在规定的条件下,建立标示值和按参考标准的测量结果之间关系的一组操作。
注1:该术语用于“不确定度”方法。
注2:原则上,标示值与测量结果之间的关系可以用校准图表示。
[GB/T 2900.77—2008,定义311-01-09]
3.4
符合性测试 conformance test
测试一个代表性的样品来确认设计和制造的设备是否满足此标准的要求。
3.5
接触放电方法 contact discharge method
试验发生器的电极保持与受试设备的接触并由发生器内的放电开关激励放电的一种试验方法。
3.6
耦合板 coupling plane
一块金属片或金属板,对其放电用来模拟对受试设备附近物体的静电放电。
HCP 为水平耦合板;VCP 为垂直耦合板。
3.7
(性能)降低 degradation(of performance)
装置、设备和系统的工作性能与正常性能的非期望偏离。
注:“降低”一词可用于暂时失效或永久失效。
[GB/T 4365—2003,定义161-01-19]
3.8
直接放电 direct application
直接对受试设备实施放电。
3.9
电磁兼容性 electromagnetic compatibility;EMC
设备或系统在其电磁环境中能正常工作且不对该环境中任何事物构成不能承受的电磁骚扰的 能力。
[GB/T 4365—2003,定义161-01-07]
3.10
静电放电 electrostatic discharge;ESD
具有不同静电电位的物体相互靠近或直接接触引起的电荷转移。
[GB/T 4365—2003,定义161-01-22]
3.11
储能电容器 energy storage capacitor
静电放电发生器中的电容器,用以代表人体充电至试验电压值时的电容量。
注:它可以是分立元件或分布电容。
3.12
EUT equipment under test
受试设备。
3.13
接地参考平面 ground reference plane;GRP
一块导电平面,其电位用作公共参考电位。
[GB/T4365—2003, 定义151-04-36]
3.14
保持时间 holding time
放电之前,由于泄漏而使试验电压下降不大于10%的时间间隔。
3.15
(对骚扰的)抗扰度 immunity(to a disturbance)
装置、设备或系统面临电磁骚扰不降低运行性能的能力。
[GB/T 4365—2003,定义161-01-20]
3.16
间接放电 indirect application
对受试设备附近的耦合板实施放电,以模拟人员对受试设备附近的物体的放电。
3.17
上升时间 rise time
脉冲瞬时值首次从脉冲幅值的10%上升到90%所经历的时间。
[GB/T4365—2003, 定义161-02-05]
3.18
验证 verification
用于检查测试设备系统(比如,试验发生器和互连电缆),以证明测试系统正常工作的一整套操作。 注1:验证的方法可能与校准方法不同。
注2:出于本基础电磁兼容标准的目的,本定义不同于 IEV 311-01-13中给出的定义。
4 概述
本部分所涉及的是处于静电放电环境中和安装条件下的装置、系统、子系统和外部设备,例如,低相 对湿度,使用低导电率(人造纤维)地毯、乙烯基服装等,这种情况存在于同电气和电子设备有关标准的 分类规定中(详细情况参见附录 A 的 A.1)。
注:从技术观点上看,这些现象的准确英语术语是“static electricity discharge”(静电放电),但是,在技术领域里和技 术文献中,广泛使用了英语术语“electrostatic discharge”(静电放电),因此,决定在本部分的英语术语标题中仍 然保留“electrostatic discharge”(静电放电)术语。
5 试验等级
表1给出静电放电试验时,试验等级的优先选择范围。
接触放电是优先选择的试验方法,空气放电则用在不能使用接触放电的场合中。表1中给出了每 种试验方法的电压。由于试验方法不同,每种方法的电压不同,这并不表示两种试验方法的严酷程度 相 同 。
有关可能影响对人体带电电压电平的各种参数的详细情况参见附录A 的 A.2。 附 录A 的 A.4 还 包括一些与环境安装等级有关的试验等级的实例。
对于空气放电试验,试验应按照表1规定的试验等级逐级实施,直至达到规定的试验等级。对于接 触放电试验,除非产品委员会有不同的规定,按照规定的试验等级实施。
附录A 中 A.3 、A.4 和 A.5 中提供了更详细的信息。
表 1 试验等级
| 接触放电 | 空气放电 | ||
|---|---|---|---|
| 等级 | 试验电压 kV | 等级 | 试验电压 kV |
| 1 2 3 4 × |
2 4 6 8 特定 |
1 2 3 4 X |
2 4 8 15 特定 |
| “×”可以是高于、低于或在其他等级之间的任何等级。该等级应在专用设备的规范中加以规定,如果规定了高 于表格中的电压,则可能需要专用的试验设备。 | |||
6 试验发生器
6.1 概述
试验发生器的主要部分包 括:
——充电电阻R ; ——储能电容器 C;
——分布电容Ca; ——放电电阻R; ——电压指示器; ——放电开关;
——充电开关;
——可更换的放电电极头(见图3); ——放电回路电缆;
——电源装置。
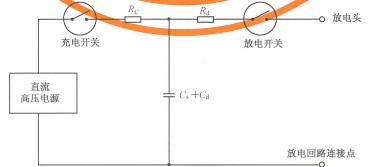
图1表示静电放电发生器的简图,未提供详细的结构图
注 1:图中 Ca 是存在于发生器和周围之间的分布电容。
注2:C4+C、的典型值为150 pF。
注3:Ra 的典型值为330Ω。
图 1 静电放电发生器简图
当按照附录B 程序评估时,发生器应满足6.2给出的要求。因此无论是图1的示意图还是参数值 均没有详细规定。
6.2 静电放电发生器的特性
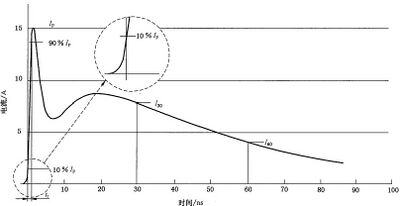
试验发生器应满足表2和表3中的规范。图2给出了表2和表3中规定的理想电流波形和测量 点。应按照附录B 中给出的方法证明符合性。
表 2 通用规范
| 参数 | 数值 |
|---|---|
| 输出电压,接触放电模式(见注1) | 至少1 kV~8 kV(标称值) |
| 输出电压,空气放电模式(见注2) | 至少2kV~15 kV(标称值)(见注3) |
| 输出电压容差 | ±5% |
| 输出电压极性 | 正极性和负极性 |
| 保持时间 | ≥5s |
| 操作放电方式 | 单次放电(见注2) |
| 注1:ESD发生器放电电极上测量的开路电压 注2:仅为了探测的目的,发生器宜能够以至少20次/s的重复频率产生放电 注3:如果最高测试电压比较低,没有必要使用有 V空文放电能力的发工器 | |
表 3 接 触放电电流波形参数
| 等级 | 指示电压 kV | 放电的第全 峰 值 电 流 ( ±1 5% ) A | 上升时间t (±25 %)ns | 在30ns时的电流 (±30%) A | 在60 ns时的电流 (±30%) A |
|---|---|---|---|---|---|
| 1 | 2 | 7.5 | 0.8 | 4 | 2 |
| 2 | 4 | 15 | 0.8 | 8 | 4 |
| 3 | 6 | 22.5 | 0.8 | 12 | 6 |
| 4 | 8 | 30 | 0.8 | 16 | 8 |
| 用于测量30 ns和60 ns处电流的时间参考点是电流首次达到放电电流第一峰值的10%。 注:上升时间t为第一个电流峰值的10%到90%的间隔时间 | |||||
图 2 4 kV 理想的接触放电电流波形
图2的理想波形方程,I(t), 如下所示:
[math]\displaystyle{ I\left(t\right)=\frac{I_{1}}{k_{1}}\times\frac{\left(\frac{t}{\tau_{1}}\right)^{n}}{1+\left(\frac{t}{\tau_{1}}\right)^{n}}\times\exp\left(\frac{-t}{\tau_{2}}\right)+\frac{I_{2}}{k_{2}}\times\frac{\left(\frac{t}{\tau_{3}}\right)^{n}}{1+\left(\frac{t}{\tau_{3}}\right)^{n}}\times\exp\left(\frac{-t}{\tau_{4}}\right) }[/math]
式中:
[math]\displaystyle{ k_1=\exp\left(-\frac{\tau_1}{\tau_2}\left(\frac{n\tau_2}{\tau_1}\right)^{1-n}\right) }[/math]
[math]\displaystyle{ k_2=\exp\left(-\frac{\tau_3}{\tau_4}\left(\frac{n\tau_3}{\tau_5}\right)^{1-n}\right) }[/math]
和
t₁=1.1 ns;t₂=2 ns;t₃=12 ns;t₄=37 ns
I₁=16.6 A( 在 4 kV);I₂=9.3 A( 在 4 kV)
n=1.8
对发生器应采取措施,以防止非期望的脉冲和连续形式的辐射或传导发射,以便使受试设备或辅助 试验设备不受额外的骚扰(参见附录 D)。
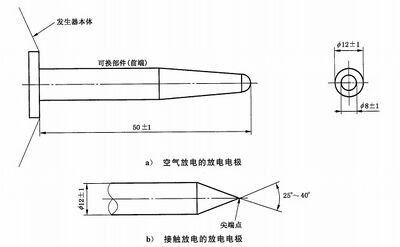
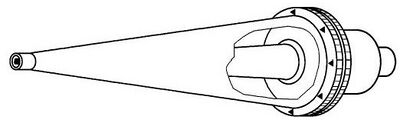
放电电极应符合图3所示的形状和尺寸。该电极可被绝缘涂层覆盖,只要产生的放电电流波形满 足规范。
图 3 ESD 发生器放电电极
对空气放电试验方法使用相同发生器,且放电开关一定要闭合。发生器应备有图3a) 所示的圆形 头。因为使用同样的 ESD 发生器,所以没有对空气放电模式有更多的规范要求。
试验发生器中放电回路的电缆长为(2±0.05)m, 其构成应使发生器满足波形的要求。放电回路电 缆的长度是从 ESD 发生器本体至连接点的末端。它应有足够的绝缘以防止在静电放电试验期间放电 电流不通过其端口而流向人员或导电表面。
测试中使用的放电回路电缆应和校准中使用的电缆是相同的或等同的。
若2 m 长的放电回路电缆不够长(例如较高的受试设备),可以采用不超过3 m 长的电缆。试验中 使用的电缆应符合波形规范。
6.3 ESD 布置的验证
验证的目的是确保 ESD 试验布置可运行。 ESD 试验布置包括:
——ESD 发生器;
——放电回路电缆;
——470 kQ 泄放电阻;
——接地参考平面;
——形成放电路径的所有连接。
图4给出了台式设备 ESD 测试布置实例,图5给出了落地式设备的实例。
要验证正确的 ESD 试验布置, 一种验证方法是观察在低电压设置时,对耦合板空气放电时产生的 小火花和在高电压设置下的大火花。在此验证之前,要验证接地带的连接和位置。
基本原理:因为来自 ESD 发生器的波形参数通常不会发生细微变化(例如:波形的上升时间和持续 时间不会漂移),最可能的失效是ESD 发生器电压未送至放电电极,或者是电压控制失效。放电路径中 的电缆、电阻或者连接导线的损坏、松脱或缺失,都会导致无法放电。
在试验前,建议先验证 ESD 试验布置。
7 试验布置
7.1 试验设备
试验布置由试验发生器、受试设备和以下列方式对受试设备直接和间接放电时所需的辅助仪器组成:
a) 对导电表面和对耦合板的接触放电;
b) 在绝缘表面上的空气放电。
试验可分为两种不同的类型:
——在实验室进行的型式(符合性)试验;
——在最终安装条件下对设备进行的安装后试验。
优先选用的试验方法是在实验室内进行的型式试验
受试设备应根据制造厂家的安装说明书(如果有的话)进行布置。
7.2 实验室试验的布置
7.2.1 试验要求
下述要求适用于8. 1中规定的参考环境条件下的实验室试验
实验室的地面应设置接地参考平面,它应是一种最小厚度为0,25 mm 的 铜或铝的金属薄板,其他 金属材料虽可使用但它们至少有0 .65mm 的厚度。
接地参考平面每边至少应伸出受试 设 备鼓水 平 耦合板 ( 适 用时)之外05 m, 并将它与保护接地系 统相连。
应始终遵守国家有关安全规程的 规 定
受试设备应按其使用要求布置和连 线。
受试设备与实验室墙壁和其他金属性结构之间的距离最小 0 .8 m。
受试设备与静电放电发生器(包括任何外部的供电电源)按照它们的安装技术条件接地。不允许有 其他附加的接地线。
电源与信号电缆的布置应能反映典型的实际安装。
静电放电发生器的放电回路电缆应与接地参考平面连接。如果这个长度超过所选放电点需要的长 度,如可能将多余的长度以无感方式离开接地参考平面放置。除了接地参考平面,放电回路电缆与试验 配置的其他导电部分保持不小于0.2 m 的距离。
注1:如果金属墙和接地参考平面电气连接,允许将放电回路电缆与试验室的金属墙连接。
每根线缆与接地参考平面的连接和所有搭接均应是低阻抗的,例如在高频场合下采用机械夹紧装 置等。
规定有耦合板的地方,例如允许采用间接放电的地方,这些耦合板采用最小为0.25 mm 厚的金属 板(铜或铝,其他金属材料也可以被使用,但是它们的厚度至少为0.65 mm), 而且经过每端带有 一个 470 kΩ电阻的电缆与接地参考平面连接。这些电阻器应能耐受住放电电压。当电缆置于接地参考平 面上时,电阻器和电缆应具有良好的绝缘,以避免对接地参考平面的短路。
注2:连接在水平耦合板和垂直耦合板(见图4~图8)接地线上的470 kΩ 泄放电阻器是用来防止静电放电发生器 对耦合板放电后,施加在耦合板上的电荷即刻消失。这增加了静电放电对受试设备的影响。在试验中,电阻器应能承受 施加到受试设备的最大放电电压。它们宜放置在靠近接地线的两端以此来形成一个分布电阻。
不同类型设备的其他技术规范在下面给出。
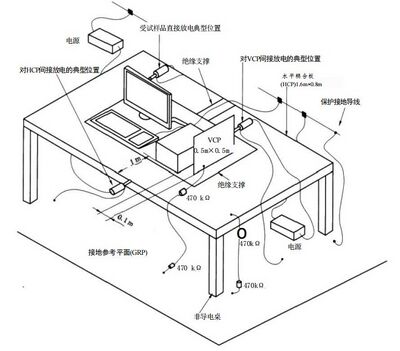
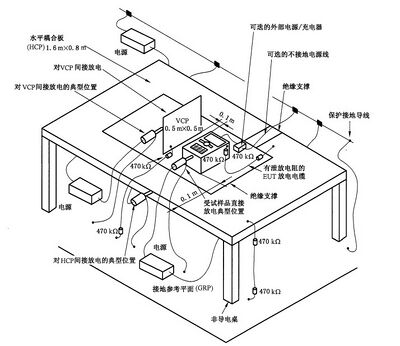
7.2.2 台式设备
试验设备包括一个放在接地参考平面上(0.8±0.08)m 高的非导电桌子。
放在桌面上的水平耦合板(HCP) 尺寸为(1.6±0.02)m×(0.8±0.02)m, 并用一个厚(0 .5± 0.05)mm 的绝缘支撑将受试设备和电缆与耦合板隔离。
注:建议保持绝缘性能。
如果受试设备过大而不能保持与水平耦合板各边的最小距离为0.1m, 则应使用另一块相同的水 平耦合板,并与第一块距离(0.3±0.02)m。 此时要将桌子扩大或使用两个桌子,这些水平耦合板不必搭 接在一起,而应经过另一根带电阻电缆接到接地参考平面上。
所有受试设备的安装脚架应保持原位。
图4提供了台式设备试验布置的实例。
图 4 实验室试验时台式设备试验布置实例
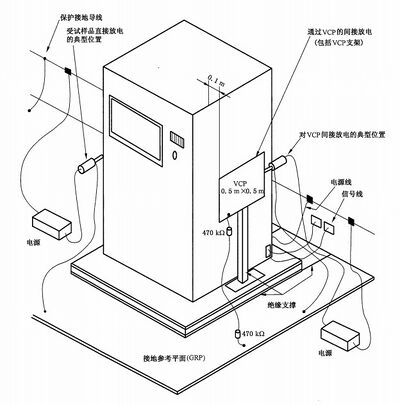
7.2.3 落地式设备
受试设备用0.05 m~0.15m 厚的绝缘支撑与接地参考平面隔开。受试设备的电缆用厚度约为 (0.5±0.05)mm 厚的绝缘支撑与接地参考平面隔开。电缆的隔离应超过受试设备隔离的边缘。
图5提供了落地设备试验布置的实例。
任何与受试设备有关的安装脚架应保持原位。
图 5 实验室试验时落地式设备试验布置实例
7.2.4 不接地设备
7.2.4.1 概述
本条描述的试验布置适用于安装规范或设计不与任何接地系统连接的设备或设备部件。设备或设 备部件,包括便携式、有或者没有充电器(电源线不接地)的电池供电设备(内部和外部)和双重绝缘设备 (Ⅱ类设备)。
基本原理:不接地设备或设备的不接地部件不能如I 类供电设备自行放电。若在下一个静电放电 脉冲施加前电荷未消除,受试设备或受试设备的部件上的累积电荷可能使电压为预期试验电压的两倍。 因此,双重绝缘设备的绝缘体电容经过几次静电放电累积,可能充电至异常高,然后以高能量在绝缘击 穿电压处放电。
试验布置应分别与7.2.2和7.2.3的描述相同。
为模拟单次静电放电(空气放电或者接触放电),在施加每个静电放电脉冲之前应消除受试设备上 的电荷。
在施加每个静电放电脉冲之前,应消除施加静电放电脉冲的金属点或部位上的电荷,如连接器外 壳、电池充电插脚、金属天线。
当对一个或几个可接触到的金属部分进行静电放电试验,由于不能保证给出产品上该点和其他点 间的电阻,应消除施加静电放电点的电荷。
应使用类似于水平耦合板和垂直耦合板用的带有470 kΩ泄放电阻的电缆,见7.2。
因受试设备和水平耦合板(台式)之间以及受试设备和接地参考平面(落地式)之间的电容取决于受 试设备的尺寸,静电放电试验时,如果功能允许,应安装带泄放电阻的电缆。放电电缆的一个电阻应尽 可能靠近受试设备的试验点,最好小于20 mm 。 第二个电阻应靠近电缆的末端,对于台式设备电缆连 接于水平耦合板上(见图6),对于落地式设备电缆连接于接地参考平面上(见图7)。
带泄放电阻电缆的存在会影响某些设备的试验结果。若在连续放电之间电荷能有效地衰减,施加 静电放电脉冲时断开电缆的试验优先于连接上电缆的试验。
因此以下选择可作为替代方法:
——连续放电的时间间隔应长于受试设备的电荷自然衰减所需的时间;
——使用带泄放电阻(例如2×470 kΩ) 的炭纤维刷清除受试设备的电荷。
注:在电荷衰减有争议时,可用非接触电场计监视受试设备上的电荷。当放电衰减至低于初始值的10%后,受试设 备被认为已放电。
图 6 不接地台式设备试验布置实例
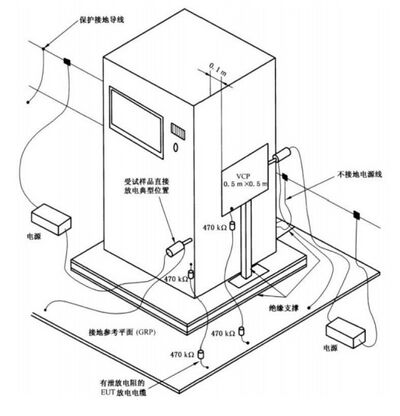
图 7 不接地落地式设备试验布置实例
7.2.4.2 台式设备
对于与接地参考平面没有任何金属连接的台式设备,安装应近似于1.2.2和图4。
对受试设备上可触及的金属部分施加静电放电,其金属部分和水平耦合板之间应使用带泄放电阻 的电缆连接,见图6。
7.2.4.3 落地式设备
对于与接地参考平面无任何金属连接的落地式设备,安装应近似于7.2.3和图5。
对受试设备上可触及的金属部分施加静电放电,其金属部分和接地参考平面(GRP) 之间应使用带 泄放电阻的电缆连接,见图7。
7.3 安装后试验的布置
对于现场进行的安装后试验,只有经制造商和用户双方同意时才能进行。 一定要考虑相邻的设备 可 能 受 到 的 不 利 影 响 。
注:此外,安装后的静电放电现场试验可能会使受试设备遭受明显的老化。 一旦承受过静电放电,许多现代电子电路的平均无故障时间(MTTF) 将显著缩短。虽然电子设备不 一 定在进行静电放电试验时立即失效,但经受过 静电放电试验的电子设备出现故障通常远比完全没有经受过静电放电试验的来得更快。考虑到这一 点,不进 行安装后现场静电放电试验可能是明智的决定。
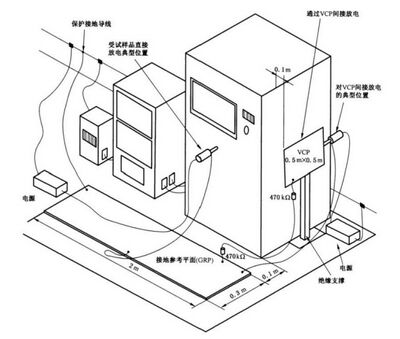
如 果 决 定 进 行 安 装 后 静 电 放 电 试 验 , 受 试 设 备 应 在 其 最 终 安 装 完 毕 条 件 下 进 行 试 验 。
为了便于放电回路电缆的连接,应将接地参考平面铺设在地面上并保持与受试设备约0.1m 的距 离,该平面应当是厚度不小于0.25 mm 的铜或铝板,也可使用其他的金属材料,但其最小厚度为 0.65 mm,安装条件允许时接地参考平面应是宽约0.3 m 和长约2m。
接地参考平面应连接到保护接地系统。如无法与保护接地系统连接,则该接地参考面应与受试设 备的接地端连接 , 如有 。
静电放电发生器的放电回路电缆应接到接地参考平面上。当受试设备安装在金属桌上时,应将桌 子 通 过 每 端 接 有 4 70 kΩ 的 电 缆 连 接 到 参 考 平 面 上 , 以 防 止 电 荷 的 累 积。
不接地的金属部件应按照7.2.4进行测试。有泄放电阻的电缆应连接到接地参考平面上,并靠近 受 试 设 备 。
图8提供了安装后试验布置的实例。
图 8 安 装 后 试 验 时 落 地 式 设 备 试 验 布 置 实 例
8 试验程序
8.1 实验室的参考条件
8.1.1 环境参数
为了使环境参数对试验结果的影响减至最小,试验和校准应在8.1.2和8.1.3规定的气候和电磁参 考条件下进行。
8.1.2 气候条件
受试设备应在预期的气候条件下工作。
在空气放电试验的情况下,气候条件应在下述范围内:
——环境温度:15℃~35℃;
——相对湿度:30%~60%;
——大气压力:86 kPa~106 kPa。
注:其他的数值只在适用于设备的特定气候环境下使用。
8.1.3 电磁环境条件
实验室的电磁环境应保证受试设备的正确运行,不应影响试验结果。
8.2 受试设备的考核
应对试验程序和软件进行选择,使受试设备进行所有正常运行方式。虽然鼓励采用专门的考核软 件,但只有证明受试设备能得到全面考核时才允许。
对于符合性试验,受试设备应在由初步试验所确定的最敏感方式下连续地运行(程序循环)。
如果要求有监测设备,那么为了减少出现故障误指示的可能性,应对监测设备去耦。
8.3 试验的实施
8.3.1 对受试设备的放电
试验应按照试验计划,采用对受试设备直接和间接的放电方式进行。它包括:
——受试设备典型工作条件;
——受试设备是按台式设备还是落地式设备进行试验;
——确定施加放电点;
——在每个点上,是采用接触放电还是空气放电;
——所使用的试验等级;
——符合性试验中在每个点上施加的放电次数;
——是否还进行安装后的试验。
为了制定试验计划,可能需要进行某种调查性试验。
注1:必要情况下需提供测量不确定度,附录E 给出了不确定度预算的报告。
注2:在测试结果有变化的情况下,附录F 给出了一个静电放电调整试验策略,来确定差异的来源。
8.3.2 ·对受试设备直接施加的放电
除非在通用标准、产品标准或产品类标准中有其他规定,静电放电只施加在正常使用时人员可接触 到的受试设备上的点和面。以下是例外的情况(亦即,放电不施加在下述点):
a) 在维修时才接触得到的点和表面。这种情况下,特定的静电放电简化方法应在相关文件中 注明。
b) 最终用户保养时接触到的点和表面。这些极少接触到的点,如换电池时接触到的电池触点、录 音电话中的磁带等。
c) 设备安装固定后或按使用说明使用后不再能接触到的点和面,例如底部和/或设备的靠墙面或 安装端子后的地方。
d) 外壳为金属的同轴连接器和多芯连接器可接触到的点。该情况下,仅对连接器的外壳施加接 触放电。
非导电(例如塑料)连接器内可接触到的点,应只进行空气放电试验。试验使用静电放电发生 器的圆形电极头。
通常,应考虑以下六种情况(见表4)。
表 4 静电放电施加在连接器上的情况
| 例 | 连接器外盖 | 涂层材料 | 空气放电 | 接触放电 |
|---|---|---|---|---|
| 1 | 金属 | 无 | 外壳 | |
| 2 | 金属 | 绝缘 | 涂层 | 可接触的外壳 |
| 3 | 金属 | 金属 | 外壳和涂层 | |
| 4 | 绝缘 | 无 | ||
| 5 | 绝缘 | 绝缘 | 涂层 | |
| 6 | 绝缘 | 金属 | 涂层 | |
| 注:若连接器插脚有防静电放电涂层,涂层或设备上采用涂层的连接器附近宜有静电放电警告标签。 | ||||
| *若产品(类)标准要求对绝缘连接器的各个插脚进行试验,应采用空气放电。 | ||||
e) 由于功能原因对静电放电敏感并有静电放电警告标签的连接器或其他接触部分可接触到的 点,如测量、接收或其他通讯功能的射频输入端。
基本原理:许多连接器端子用于处理模拟或数字的高频信息,因而不能使用充分的过压保护装置。 过压保护二极管的寄生电容妨碍受试设备工作频段内的工作。对于模拟信号,带通滤波器可能是解决 方案。
在上述情况中,推荐的特定静电放电简化步骤应在相关文件中注明。
最后的试验值不应超过产品的规范值,以避免损坏设备。
试验应以单次放电的方式进行。在预选点上,至少施加十次单次放电(最敏感的极性)。
注1:最小放电次数取决于受试设备,有同步回路的设备需要更多的放电次数。
连续单次放电之间的时间间隔建议为1s, 但为了确定系统是否会发生故障,可能需要较长的时间 间隔。
注2:放电点通过以20次/s 或以上放电重复率来进行试探的方法加以选择。
静电放电发生器应尽可能保持与实施放电的表面垂直,以改善试验结果的可重复性。如果静电放 电发生器不能和施加表面保持垂直,放电采用的测试方法应记录在报告中。
当实施放电的时候,发生器的放电回路电缆与受试设备的距离至少应保持0.2 m, 并且操作者不能
手持放电回路电缆。
在接触放电的情况下,放电电极的顶端应在操作放电开关之前接触受试设备。
对于表面涂漆的情况,应采用以下的操作程序:
如设备制造厂家未说明涂膜为绝缘层,则发生器的电极头应穿入漆膜,以便与导电层接触。如厂家 指明涂漆是绝缘层,则应只进行空气放电。这类表面不应进行接触放电试验。
在空气放电的情况下,放电电极的圆形放电头应尽可能快地接近并触及受试设备(不要造成机械损 伤)。每次放电之后,应将静电放电发生器的放电电极从受试设备移开,然后重新触发发生器,进行新的 单次放电,这个程序应当重复至放电完成为止。在空气放电试验的情况下,用作接触放电的放电开关应 当闭合。
8.3.3 间接施加的放电
8.3.3.1 受试设备周围物体的放电
对放置于或安装在受试设备附近的物体的放电应用静电放电发生器对耦合板接触放电的方式进行 模拟。
除了8.3.2中论述的程序之外,还需满足8.3.3.2和8.3.3.3中所提出的要求。
8.3.3.2 在受试设备下面的水平耦合板
对水平耦合板放电应在水平方向对其边缘施加。
在距受试设备每个单元( 若 适 用中 心 点 面 的 处 水 平耦合板近缘,至少施加 10次单次放电 (以最敏感的极性 )。放电时。放电电极的长轴药 水 平 耦合板应处于同平面,并与水平耦合板的边缘 垂直。
在放电开关闭合前,放电电极应接触水平耦合 板的 边缘(见图 1 )
产品标准可能要求对受试设备的所存面都施加放电试验。
8.3.3.3 垂直耦合板
对耦合板的一个垂直边的中心至少施加10次的单次放电(以最敏感的极性)(图4和图5),应将尺 寸为0.5 m×0.5m 的耦合板平行于受试设备放置且与其保持0. 1m 的距离。
放电应施加在耦合板上,通过调整耦合板位置,使受试设备四面不同的位置都受到放电试验。垂直 耦合板的放置被认为覆盖了受试设备0.5 m×0.5m 的 表 面。
9 试验结果的评价
试验结果应依据受试设备在试验中的功能丧失或性能降低现象进行分类,相关的性能水平由设备 的制造商或需要方确定,或由产品的制造商和购买方双方协商同意。推荐按如下要求分类:
a) 在制造商、委托方或购买方规定的限值内性能正常;
b) 功能或性能暂时丧失或降低,但在骚扰停止后能自行恢复,不需要操作者干预;
c) 功能或性能暂时丧失或降低,但需操作者干预才能恢复;
d) 因设备硬件或软件损坏,或数据丢失而造成不能恢复的功能丧失或性能降低。
由制造商提出的技术规范可以规定对受试设备产生的某些影响是不重要的,因而是可接受的试验 影响。
这种分类可以由负责相关产品的通用标准、产品标准和产品类标准的专业标准化技术委员会作为 明确表达功能准则的指南。在没有合适的通用、产品或产品类标准时,可作为制造商和购买方协商的性能规范的框架。
10 试验报告
试验报告应包括能重现试验的全部信息。特别是下列内容:
——第8章要求的在试验计划中规定的项目内容;
——受试设备和辅助设备的标识,例如商标、产品型号、序列号;
——试验设备的标识,例如商标,产品型号,序列号;
——任何进行试验所需的专门环境条件,例如屏蔽室;
——进行试验所需的任何特定条件;
——制造商、委托方或购买方规定的性能水平;
——在通用、产品或产品类标准中规定的性能要求;
——试验时在骚扰施加期间及以后观察到的对受试设备的任何影响, 及其 持续时间;
——试验通过/失败的判断原因(根据通用标准、产品标准或产品类标准 规 定的性 能 判 据 或 制 造 商 和 购 买 方达成的协议);
——采用的任何特殊条件,例如电缆长度或类型,屏蔽或接地,或受试设备 运行条件,均要符合 规 定 ;
—— 气 候 条 件 ;
—— 试 验 配 置和 受试设备布置的图纸和 或 图
附 录 A
(资料性附录) 说 明
A.1 一般的考虑
保护设备免受静电放电影响的问题对制造厂和用户来说都是相当重要的。
随着微电子元件的广泛应用,为了提高产品和系统的可靠性,迫切需要确定这一问题的各种因素, 寻找一种解决方法。
静电的累积以及随后放电的问题由于不可控制的环境条件以及设备和系统在厂矿中的广泛使用而 变得更加令人关切了。
无论什么时候人员对附近物体发生静电放电时,设备都可能遭受电磁能量的侵害。此外,放电还可 能在设备附近的金属物体之间,如桌椅之间发生。但是,根据目前得到的有限经验,可以认为,本部分阐 明的一些试验足够模拟后者现象的影响。
操作人员放电的影响可以是单纯地使设备误动作或电子元件损坏。其主要影响可以认为是由放电 电流的参数引起的(上升时间、持续时间等)。
对这个问题的认识以及需要某种手段来防止静电放电对设备非期望的影响,促使我们制定这个标 准中的标准试验程序。
A.2 环境条件对充电量的影响
合成纤维与干燥的气候相结合特别有助于静电电荷的产生。充电过程的变化有多种可能性, 一种 常见的情况是某操作者在地毯上面走动,每走一步将其身体上的电子传给化纤织物或从化纤物上获得 电子,操作者的衣服与其座椅之间的摩擦也会产生电荷的交换。操作者的身体可能被直接充电或静电 感应,在后者的情况下,除非操作者是充分通地的,否则,即使导电的地毯也不会对其提供任何保护。
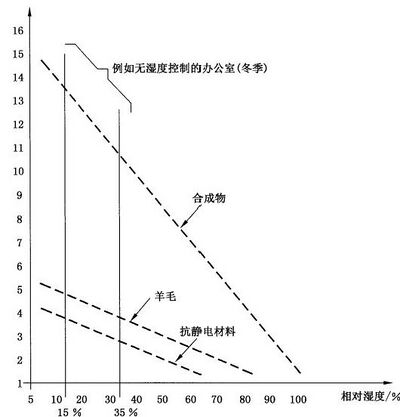
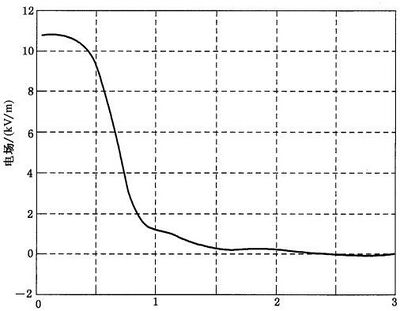
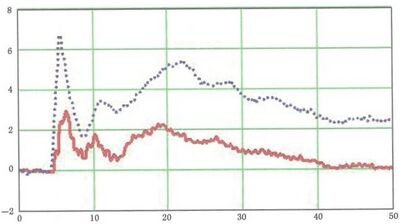
图 A.1 的曲线表示,由大气的相对湿度决定不同纤维的充电电压值。
视合成纤维的种类和环境的相对湿度而定,设备直接遭受放电的电压值可能高达几千伏。
图 A.1 与 A.2 所提到的材料接触时操作者可能被充电静电电压的最大值
A.3 环境级别与空气和接触放电的关系
作为一种可测量的量,一直将实际环境中得到的静电电压电平作为抗扰度要求,但是,现已证明,能 量转移与其说是放电之前存在的静电电压的函数,不如说是放电电流的函数。此外,还发现在较高的电 压电平范围内,放电电流一般不与预放电电压成正比。
预放电电压与放电电流之间的非正比关系的可能原因是:
——高压电荷的放电一般经过使上升时间增加的长电弧通道来实现,因此使得放电电流中的高频 分量低于与预放电电压成正比例的值。
——假定在一个典型的充电过程中充电量为常数,那么高充电电压电平更可能出现在小电容量的 情况,反之,大电容两端的高充电电压则需有一系列连续发生的过程,而它不太可能发生,这意 味着用户环境中所获得的高充电电压下电荷能量有变成稳定的趋向。
由以上得到的结论,对于某个给定的用户环境、抗干扰要求根据放电电流的大小来确定。
弄清了这个概念后,测试装置的设计就变得容易了。可通过对充电电压和放电阻抗的合理选择得 到所希望的放电电流幅值。
A.4 试验等级的选择
试验等级应按照最切合实际的安装和环境条件来选择,表 A.1 中提供了一个指导原则。
表 A.1 试验等级选择的导则
| 级别 | 相对湿度 % | 抗静电材料 | 合成材料 | 最大电压 kV |
|---|---|---|---|---|
| 1 | 35 | × | 2 | |
| 2 | 10 | × | 4 | |
| 3 | 50 | × | 8 | |
| 4 | 10 | × | 15 |
所推荐的安装与环境的级别与第5章列出的试验等级有关。
对于某些材料如木材、混凝土和陶瓷,其可能的电平不大于2 级。
当考虑选择一个适用于特殊环境合适的试验等级时,弄清静电放电效应的关键参数是十分重要的。
最关键的参数也许是放电电流的变化速率,它可通过充电电压峰值放电电流和上升时间的不同组 合来获得。
例如,利用本部分规定的静电放电发生器接触放电的8 kV/30A 第 4 级试验就足以满足15 kV 合成材料的环境对静电放电的要求。
但是,在非常于燥环境下的合成材料,则会出现高于15 kV 的电压。
在试验设备具有绝缘表面的情况下,年 使 用地 压高达15kV 的空气放电方 法。
A.5 试验点的选择
例如,所考虑的试验点可 包括以下位置
——与地绝缘的金属外壳 主 的些 点。
——控 制 或键盘区域任何点和天机通讯的其他任何点: 如 开 关 键 旋 钮按钮指示器、发光二极管 (LED) 、 缝隙、栅格、连接器罩等以及其低 操作人员易于接近的区域。
A.6 使用接触放电方法的技术原理
一般而言,上述试验方法( 空气放电)的再现性受放电头接近速度,湿度和武验设备结构的影响,并 导致脉冲上升时间、放电电流幅度的差异。
在静电放电试验中的空气放电,静电放电的情况是利用充电的电容器通过放电电极头对受试设备 的放电即放电头在受试设备表面上形成一个火花间隙来模拟的。
这种火花放电是一种非常复杂的物理现象。现已查明,在移动火花间隙的情况下,当接近速度变化 时,由此产生的放电电流的上升时间(上升速率)能从小于1 ns 和大于20 ns 发生变化。
即使保持接近速度不变,也不会使上升时间不变。对于电压和速度的某些综合影响,上升时间受到 的影响可高达30倍。
注:空气放电能在高等级电压中产生多个连续放电。
目前通常所知的能产生可重现和快速上升的放电电流的触发装置是继电器。继电器应有足够的耐 压和单次接触性(以避免上升部分的两次放电),对于较高的电压,真空继电器证明是有用的。经验表 明,利用继电器作为触发装置,不仅测量的放电脉冲在其上升部分的可重复性要好得多,而且用实际受 试设备作试验的结果重现性也更好的。
继电器启动脉冲试验装置是一个能产生特殊电流脉冲(幅值和上升时间)的装置。
这个电流与实际静电放电电压有关,如 A.3 所述。
A.7 静电放电发生器元件的选择
人体电容量的储能电容器,该电容量标称值为150 pF。
为表示人体握有某个如钥匙或工具等金属物时的源电阻可选用一个330Ω的电阻,现已证明,这种 金属放电情况足以严格地表示现场的各种人员的放电。
A.8 关于发生器规范的基本原理
当对实际受试设备施加静电放电试验时,假定有很多原因是造成复现性试验的差异。试验配置,校 准问题等,已被考虑并在本部分提出
已经考虑到改变静电放电发生器规范,但在本部分中没有提出任何改变 。以下是对做出这一决定 理由的汇总。
与发生器规范有关的,可能导致复现性问题的两个原因:
●在第一个峰值后发生器产生的放电电流波形,例如2 ns 和60 ns 之间;
● 当静电放电施加到受试设备上时发生器产生的辐射电场。
第一个原因由标准维护工作组处理,并规定与图?的2ns 至60 ns 的理想波形可有35%的容差。 在此标准的制定中,放电电流规范的潜在变化被进少调整为控制第一个峰值下 降到初始峰值的 60% 的时间为(2.5±1 )ns。
在三个不同的实验室,对不同受试设备使质种类型的发生器进 行 系列测试。 一种发生器符合
IEC 61000-4-2(E1.0),另一种类型增加了上述总金的规范 种类型的五个不同的发生器由五个不同 制造商提供。
修改的静电放电发生器一系列测试的结果忽结如 下
——使用不同的静电放电发生器进行测试时,所关注的受式设备受到影响的试验电平有所不同;
——在时域和频域中,修改的放电波形的确改善了放电电流波形;
——然而,新的波形没有给实际受试样品测试结果的复现性带来任何显著改善 。
已考虑了第二个原因然而,在不能保证辐射电场这个参数就是引起复现性问题原因的情况下,要 进行进一步系列测试需要耗费很大资源。量化辐射场对实际受试样品的影响和了解如何控制影响测试 结果复现性的相关参数还需大量的技术研究。
本部分中包含的变化认为是能够提升测试的复现性。进一步的研究可能在此标准以后的版本中提 出,来评估辐射电场对复现性的影响。
附 录 B
(规范性附录)
电流测量系统的校准和放电电流测量
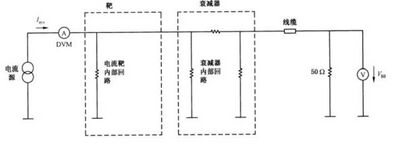
B.1 电流靶规范——输入阻抗
用来测量 ESD 发生器放电电流的同轴电流靶的输入阻抗(在内电极和地之间测量),在直流情况不 应大于2. 1Ω。
注1:靶是设计用于测量注入到理想接地平面的静电放电电流。为了减少由理想导电平面和靶的输入阻抗之间的 差异造成的误差,输入阻抗被限制在2.1Ω。但是如果靶的输入阻抗过低,输出信号将会非常小,由于耦合到电缆和示波器的原因造成误差。此外,当使用一个过低的电阻值时,寄生电感变得更加严重。
注2:输入阻抗和转移阻抗(Z,B.3) 可在直流或低频率下高精度测量得到。
B.2 电流靶规范——插入损耗
B.2.1 测量链
没有直接规定同轴电流靶的插入损耗,而是规定了包括靶、衰减器和电缆的测量链路的插入损耗。 这简化了测量系统的特性,因为只有这个链和示波器需要有特性参数,而不是每个单独的部分。
靶-衰减器-电缆链的插入损耗的变化不应超过:
±0.5 dB,1GHz 及以下
±1.2 dB,1 GHz~4 GHz
关 于S21插入损耗的标称值为:
Sa=20 log[2Zy/(Rm+50 Ω)]dB,Rm是靶-衰减器-电缆链带50Ω负载的直流输入阻抗。
注1:不同的校准时间间隔可用于直流传输阻抗和更多涉及到插入阻抗的计算。如果一个重复的直流传输阻抗测 量结果表明它和原来的测量结果相差不到1%,如果使用了相同的电缆和衰减器而没有其他迹象(例如连接 器松动或损坏),用户可以认定靶-衰减器-电缆链的插入损耗没有变化。
注2:靶-衰减器-电缆链应始终视为一个整体。一旦一个部分变化了,或是拆解和组装,全链需要重新校准来确保 符合规范要求。
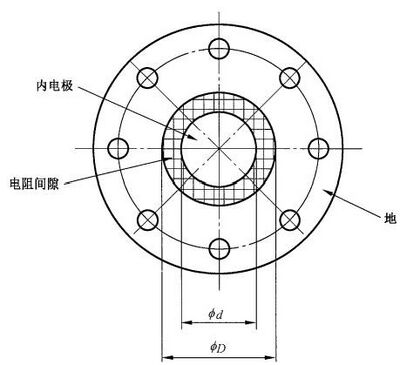
B.2.2 靶适配线
图 B.1 显示靶适配线连接了50Ω的同轴电缆至静电放电电流靶的输入。几何上来说,能很顺利的 扩大同轴电缆的直径至靶的直径。如果靶的制造按照直径比“d”至“D”( 见 图 B.2)来计算插入阻抗而 不等于50Ω时,靶适配线应被做成内部导体的外直径等于电流靶内电极的直径。用填充锥形适配线的 材料(通常为空气)的介电常数来计算阻抗。靶适配线应在4 GHz 带宽下保持(50±1)Ω。两个面对面 放置的靶适配线的回波损耗至1 GHz 时应优于30 dB, 至4 GHz 时,应优于20 dB, 总插入损耗至4 GHz 时应少于0.3 dB。
注:除了圆锥形,可接受其他形状。
图 B.1 靶适配线连接到电流靶的实例
bd——内电极外径; *D——地结构内径。
图 B.2 电流靶正面图实例
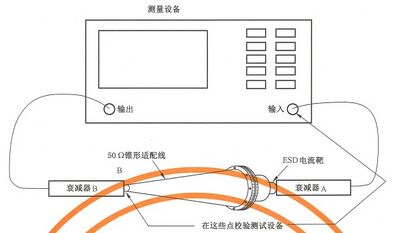
B.2.3 靶-衰减器-电缆链的插入损耗的确定
使用一 台矢量网络分析仪(VNA) 来测量链路的插入损耗。如果能够达到足够的精度要求,也可以 使用其他测量标量插入损耗的系统。
测量插入损耗的程序如下:
● 校准网络分析仪的校准点如图 B.3 所示(衰减器和靶之间和衰减器和靶适配线之间)。
注1:如果没有使用网络分析仪,程序需进行相应的修改。
注2:除了直流,宜使用网络分析仪的最低频率。直流特性分开测量。
注3:两个适配线或适配线和靶的中心接触的稳定性宜通过反复测量,使用不同中心线角度断开和重新连接装置来 验 证 。
● 图 B.3 显示连接和插入靶适配线至靶-衰减器(≥20 dB)-电缆链。
● 测量插入损耗。
插入损耗的变化应满足 B.2 的要求。
图 B.3 电流靶-衰减器-电缆链插入损耗测量的实例
B.3 靶-衰减器-电缆链的低频率转移阻抗确定
靶-衰减器-电缆链的低频转移阻抗定义为注天到靶输人端的电流和电流输出端50Ω精密负载上 的电压之比(例如放置在电缆一端,替代示波器的锁载
在一次静电放电测量中如果靶的输入 就为 I 示波器显示的电压为Vocs。从显示的电压来计 算未知的电流,电压被低频率系统的转移阻抗Z,分压了。
图 B.4 确定低频系统转换阻抗的电路图
注1:这仅是靶内部电路图的一个实例。其他内部电路也可以。
靶-衰减器-电缆链的低频系统转移阻抗可通过如下确定:
● 用一个接近1A 的注入电流 Isys注入到电流靶的正面。正面是产生放电的那一个面。
● Zsys是发生器校准的关键参数。50Ω负载的最大误差为±1%。
● 测量通过50Ω精密负载的电压Vso。
●通过如下公式来计算转移阻抗:
[math]\displaystyle{ Z_{y}=\frac{V_{50}}{I_{y}} }[/math]
注2:为了验证热电压不影响结果,测量可以分别用正负电流。两个结果之间相差小于0.5%。 可用其他方法来确定整个靶-衰减器-电缆链的转移参数。
B.4 静电放电发生器的校准
B.4.1 校准结果
可比较的静电放电校准结果是十分重要的。尤其当测试使用的静电放电发生器是不同的制造商, 或当测试预计会持续一个很长的时间。重要的是,在评估中重复性是一个重要的推动因素。静电放电 发生器应在规定的时间间隔内,有认可的质量保证体系下进行校准。
注:本附录的过程适用于校准的目的。适用于测试前验证发生器的不同程序在6.3中提及
静电放电发生器的校准应在8.1.2中规定的环境条件范围下进行。
B.4.2 静电放电发生器校准所需的测试设备
静电放电发生器校准所需设备如下:
● 有足够带宽的示波器(≥2GHz 模拟带宽);
● 同轴电流靶-衰减器电缆链;
● 测量至少 1 5kY 电 压的高压计。可能需要使用一个静电电压表来避免带载的输出电压;
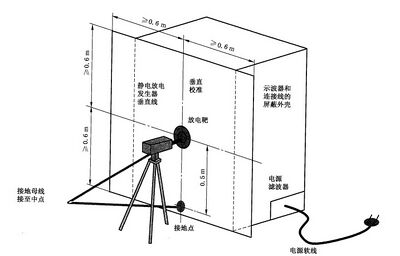
● 安装在垂直校准平面的同轴电流靶、靶和平面的任何边缘至少有0.6m;
● 衰减器需要有足够的功 率
注:附录C 给出了合适的同轴电流靶的实例
B.4.3 接触模式发生器校准的程序
电流靶应安装在满足 B.4.2 的垂直校准平面中心。静电放电发生器的放电回路电缆(接地线)应连接在平面中心底部低于靶 0.5 m 处,接地线应在电缆中心向后拉,形成一个等腰三角形。校准时,接地线不应平放在地板上。 安装如下步骤验证静电放电发生器的电流波形是否符合规范。记录波的形状和测量如下参数: I,峰值放电电流,单位为安培(A); Im从到达峰值电流 I,的 0.1 倍电流值处开始,30 ns 后的电流值,单位为安培(A); I...从到达峰值电流 I。的 0.1 倍电流值处开始,60 ns 后的电流值,单位为安培(A); t,电流的上升时间,单位为纳秒(ns)。
表 B.1 接触放电校准程序
| 步骤 | 说明 |
|---|---|
| 按照表1定义ESD发生器在每个测试等级正负极性各放 电5次,存储每个结果 | 所有5次放电应满足规格 |
| 测量每个波形的I。,I,Imt | 对每个测试等级的参数都应检查 |
| 30 ns时的电流 检查I30是否是2A±30% | 对每个测试等级的参数都应检查 |
| 60 ns时的电流 检查I60是否是1A±30% | 对每个测试等级的参数都应检查 |
| 峰值电流 检查Ip是否是3.75 A±15% | 对每个测试等级的参数都应检查* |
| 上升时间 检查tr,是否为0.8 ns±25% | 对每个测试等级的参数都应检查 |
| *这份表格中给出的电流值对应的电压为1kV。这些测量值和产生的电压成正比 | |
注1:发生器宜安装在三脚架或等效的非金属低损耗的支撑物上。
注2:发生器宜以试验时相同的方式供电。
注 3:相比图B.5的相反配置也可以使用。
图 B.5 静电放电发生器性能校准的典型配置
如果能证明测量系统上的间接耦合路径不会影响校准结果,那么没有必要屏蔽示波器。
当如下情况时如果示波器结果没有任何触发,校准系统可认为有足够的抗扰度(即没有必要用法拉 第笼):
●示波器的触发电平设置小于等于最低测试等级的10%,
●和静电放电发生器对靶的外圈(不是内圈)进行最高等级的放电。
附 录 C
(资料性附录)
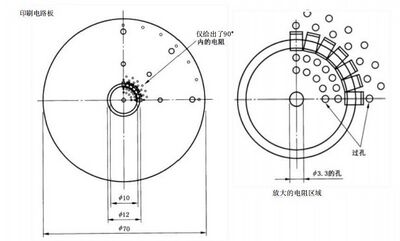
满足附件 B 要求的校准靶实例
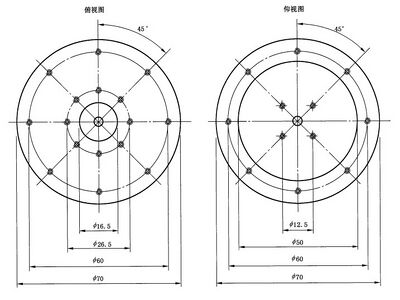
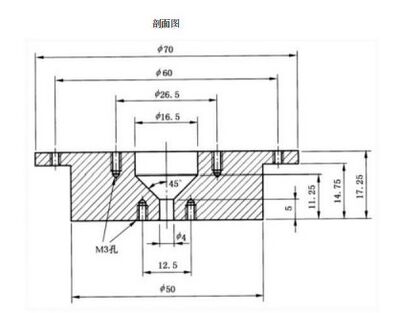
图 C.1~ 图 C.5 给出了满足附录B 要求的靶的详细构造。当使用1m 长 的 RG400 电缆时应具有 平坦的插入损耗。建议使用20 dB 或更大的衰减器直接连接到校准靶的输出端口来避免多次反射。
注:图C.1~图C.5 为实例,因此没有给出公差。
中央黄铜部分——大约1:1
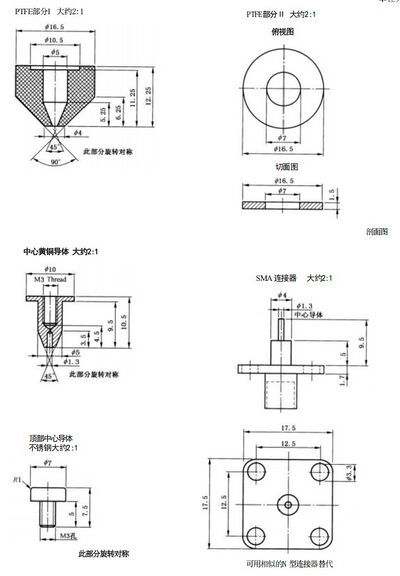
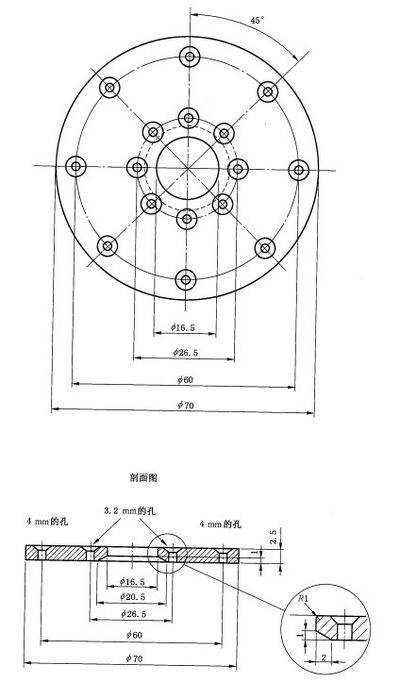
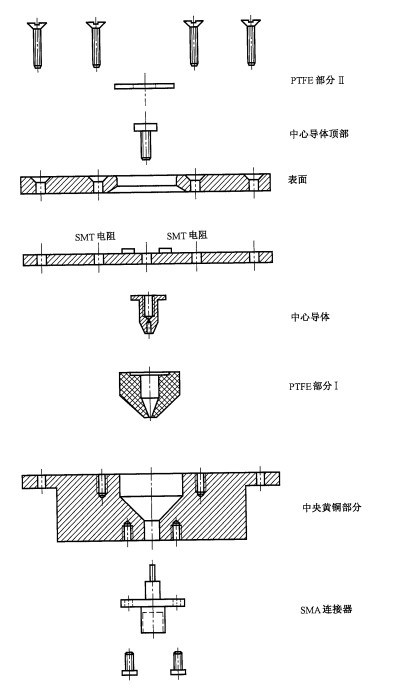
图 C.1 同轴靶的机械图
图 C.1(续)
说 明 :
电 阻 尺 寸 —— 0805 ;
电 阻 值 ——51Ω;
位 置 —— 能 被 接 触 的 , 完 全 对 称 的 ( 使 用 模 板 ) ;
材 质 ——0.5 mm FR-4,镀 金 ;
过 孔 —— 电 阻 每 边 的 两 个 孔 环 连 接 到 印 刷 电 路 板 的 外 缘 孔 。 大 约 需 要 2 5 个 电 阻 。
图 C.2 同轴靶的机械图
图 C.3 同轴靶的机械图
图 C.4 同轴靶的机械图
图 C.5 同轴靶的机械图
附 录 D
(资料性附录)
人体金属放电和静电放电发生器产生的辐射场
D.1 试验过程中产生的有意无意场概述
D.1.1 总 则
人体静电放电(通过一个小型的手持金属片)是本部分及之前版本中规定的电流波形的基础。人体 和 ESD 发生器放电都会产生与之相关的强电磁场
下面的子条款首先回顾了人体放电的过程,然后回顾了由静电放电发生器放电的过程。
D.1.2 人 的静电放电
人对受试设备 所产 生的静电放电,会发生下面一系列的事件:
a) 当手排金属片接近受试设备的金属表面,在放电电流产生前,静电场就存在了。这个时候没有(或十分少电流流动,也不存在相关的磁场
b) 手持金属部件与受试设备之间一旦开始放电,两者之间放电间隙内的静电场骤然下降。在50 ps~5ns的时间内,放电间隙两端电压从初始值骤然下降至大约25 V40V。 骤然下降 的时间取决于电弧参数电压等。电场的骤然下除是引起强瞬变电磁场的一系列事件中的第 一步 。
c) 电流开始在人手持金属部分和受试设备上流动。初始电流以光速扩展并在大约8 ns 内到达 人的胳膊。电流在受试设备和胳膊持续软展由 于 辐射 和 电 阻 的 原 因,会发生反射和衰减,导 致在受试设备和人两者上有电流密度的复杂型态
d) 随 着放电过程的持续,电流的最高频率分量会很快因为辐射而衰减。 随着 时间的增加电流会 变得平骨(即具有更少的高频分量),最后受试设备和人体之间达到一个新的静电平衡。然而, 因为在人体上的电荷完全泄放完毕之前电弧可能已经消失,留在人体上的剩余电荷就有可能 不为零。如果手和金属体再次接近受试器件,就可能在更低电压下产生第二次放电,导致一系 列的静电放电出现。与每次更低电压的放电对应,就有更快的上升时间(部分归因于更低的 电 压 ) 。
e ) 在每次一系列的静电放电中,在手臂、人体或受试设备适当点放置监测器,可测得放电前电荷 密 度、放电中快速变化电流和放电后少量剩余电 荷。
f) 从天线理论可知,变化的电荷密度和变化的电流将产生辐射场。近距离场由电流和电荷直接 决定,距离上更远的场则由电流和电荷对时间的导数决定。近距离场(近场)和在更远距离观 察到的场(远场)之间的转换区域,情况更复杂。测量和仿真结果表明:至少在具有最多干扰的 前几纳秒里,静电放电的瞬态场将在距离电弧10 cm 处达到远场条件。
g) 由上所述显然可见,在考虑关于电子系统非破坏性故障时,电流和电荷对时间的导数是极其重要 的 。
h) 重要的是,在人体放电中,电流和电荷对时间的导数是由电弧内电压的突降时间决定的。因 此,放电电流的上升时间决定了高频分量。
总之,人体-金属静电放电的瞬态场是静电放电过程的重要部分。理想的静电放电发生器,应能够 以一定量化方式重现瞬态场。至于人体-金属静电放电的场强等参量,已为业界所熟悉。
D.1.3 静电放电发生器
下一步就是分析和比较现有静电放电发生器中出现的过程。由于大部分静电放电试验是由接触模 式产生的,考虑到复现性,下列所述仅限于接触模式的静电放电发生器:
a) 静电放电发生器的放电尖端接触到受试样品的接地部件(大部分情况下)。
b) 放电前,静电放电发生器中的电容充完电。在许多设计中,在充电过程产生的大部分静电场被 限制在静电放电发生器内。于是,在放电前附近的静电场比在同一点由人体充电有相同电压 时测量的静电场小得多。
c) 放电是由静电放电发生器内部继电器的闭合启动的。这种特殊继电器的设计决定了放电电流 良好的复现性。然而继电器是内部的而不是在静电放电发生器接触受试样品的点上,所以初 始的放电电流 流动和人体放电明显不 同。
d) 继电器内的电压骤然下降时间非常快,肯定小于100 ps, 导致电流波从继电器向各个方向和各 个能接触到的金属部件和其他接近金属部件传播。电流波将以光速传播(绝缘体中会降低速 度)。电流波形的 上升时间和电压骤然下降时间相等。
e) 电压的骤然下降时间小于100 ps,但此标准要求在靶的接触点测得的电流上升时间为(0.8±0.2)ns .为了 达到 此目标,静电放电发生器里采取了措施,使得继电器内非常低的上升时间值 在放电尖端达到标准值。
f) 瞬态场是由所有电流和电荷密度对时间导数引起的。发生器产生的放电和人持金属产生的放电有一点重要区别要注意:对于人体放电,电弧上电流的上升时间是最快的过程,而且它决定 了睡态场的频谱。然而,静电放电发生器接触放电模式下的高频频谱取决于继电器电压的塌 缩,而不是放电 尖端的电流上升 时间
g) 由于发生器中所有变化的电流引起瞬态场,继电器100 ps 的上升电流会引起静电放电发生 器的瞬态场,放电点 0.810.2) ns 上升电流也会引起瞬态场。发生器中由便快事件引起的 瞬态场通常不是期望的瞬态场,因为它们增加的辐射场高频分量超过了由在放电点上具有相同的电流上升时间和峰值的等效人至金属放电所产生的辐射场高频分量。
综上所示,快速上升电流对瞬态场的影响程度依赖于静电放电发生器的设计。在任何给定的发生 器中,这个场的影 响可能 被抑制得很好或者也可能来决定瞬态场。本部分不规定这些因素,可能会造成 静电放电试验中的故障事件高度依赖于所使用的特定发生器。
D.2 受试设备对于静电放电的反应
在静电放电试验中,测试了受试设备对于宽范围的电子骚扰的响应。范围包括:电介质击穿电压, 远离注入点间隙处的二次击穿,RI 跌落的电流,Ldz /dt 跌落的磁场,感应电压产生的磁场和感应电压 产生的电场(场既可以是远场也可以是近场)。在这方面,静电放电试验不同于 EMI 测试,它把多重试 验变成一个试验。
由于受到静电放电试验的不同骚扰导致受试设备失效的例子:
——在连接器针脚上的放电导致IC 的故障;
在这个例子中,能量释放在IC 上,流过IC 上的最大电流或电荷最有可能决定损坏的阈值;
——通过塑料外壳上空隙的放电形成的火花到达了IC;
在这种情况下,静电放电试验确定了穿过塑料缝隙的间隙的电介质击穿强度。
——对机箱的放电导致机箱内系统的故障。
在这个例子中,最有可能的是静电放电事件的瞬态场耦合到印制线、线缆或直接进入系统的 IC, 引 起的电压或电流会扰乱系统的逻辑功能。
甚至在如20 cm 这样的适当距离,静电放电发生器内的电流到场的耦合机制是由电流时间导数决 定的。此外,场和受试样品中线、印制线或IC 的耦合是 一个电场和磁场的变化率的函数。总结:包括场 建立中和感应过程中的时间导数造成了注入电流,这导致了放电尖端不同的电流脉冲波形和由场造成 的印线里不同的感应电压。典型的印线里感应电压宽度比本部分提及的静电放电初始电流窄得多,而 且它们可能会现出振铃性。
由于瞬态场依赖于特定静电放电发生器的设计(特别是在频率300 MHz 以上的场能量分量),我们 需要预期在印制线、线上或IC 内的感应电流会受到静电放电发生器具体设计的强烈影响。如果同样的 受试样品测试时使用不同的静电放电发生器且静电放电发生器的制造商没有采取措施以尽量减少由继 电器内快速电压塌缩引起的不需要的电磁场部分,这将会导致测试结果有很大的变化(大部分情况下是 系统故障,而不是破坏)。请注意,这些测试结果的差异只发生在受试设备对高频敏感的情况下,主要大 于 1 GHz。
D.3 静电放电瞬态场的参考事件
已测量的人体金属静电放电瞬态场在5 kV 电压时的上升时间为850 ps。 一 个理想的静电放电发 生 器 宜 能 在 5 kV 接触模式试验下重现瞬态场。为了获取数据,宽带场强探头(1 .5 MHz~1.5 GHz为±1 dB)要放置在垂直参考平面上距离放电点(即靶位置)0.1 m 处(见图 D.1)。
图 D.1 充 电 电 压 5 kV, 测量距离0 . 1m, 弧长0.7 mm, 人持金属放电时的实测电场
静电场在电场中占主导地位,电场的跌幅达到静电场初值的20%的下跌时间近似于电流的上升 时 间 。
图 D.2 是基于上升时间500 ps 放电电流的磁场的实例。
图 D.2 充电电压5 kV, 测量距离0.1m, 弧长0.5 mm, 人持金属放电时的实测磁场
磁场波形遵循电流波形。
静电放电发生器产生的场波形中可能出现的问题是振铃特性。静电放电发生器产生的场强可能远 小于或远大于人/金属场的波形,这个很大程度上取决于静电放电发生器和接地线对场强探头之间的 角 度 。
D.4 小环上的感应电压
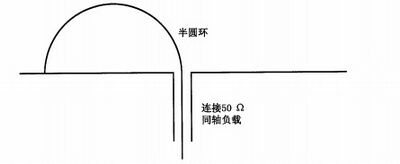
静电放电产生的瞬态场会在PCB 上的印制线上产生感应电压。如果把一个小环放置在接地平面 上,瞬态场高频分量可以无需校准的宽带场强探头就可测量推导出,而且这比场测量更加直接的反应了 感应到印线过程。图 D.3 给出了试验布置。
图 D.3 接地平面上的半圆环
图 D.3 中环的半径是14 mm 。线的直径是0.7 mm 。环放置在距静电放电发生器0.1m 处。
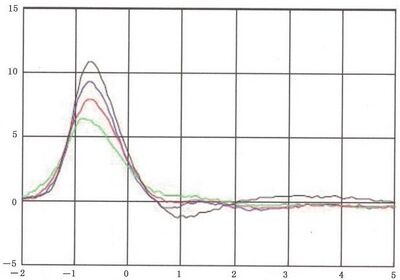
图 D.4 所示是人金属静电放电的典型感应电压在5 kV、上升时间大概在850 ps
图 D.4 半环上的感应电压(纵坐标改为感应电压)
在图 D.4 中,半径14 mm 的环放置在离人金属静电放电(5 kV, 上升时间大约为850 ps, 电弧长为 800 um)0.1 m 处。半环的负载为50Ω。
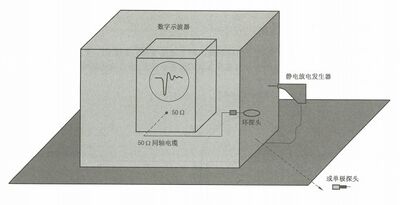
D.5 用商用的场探头和静电放电发生器测量静电放电所产生的辐射场
图 D.5 给出了测量静电放电辐射场的试验布置。
图 D.5 测量静电放电辐射场试验布置实例
为了测量电场和磁场,应使用下列仪器:
● 带宽至少2 GHz 的数字存储示波器;
●一组商用磁场探头(带屏蔽电场的小环)和电场探头(小的单极天线);
● 50Ω同轴电缆;
● 静电放电发生器。
测量布置(见图D.5):
●测量宜在屏蔽室内进行(如果环境没有产生重大影响则不必要使用);
● 静电放电发生器设置在5 kV;
●静电放电电流宜根据本部分提及的布置测量来与静电放电数学参考波形比较:
●数字示波器宜放置在屏蔽壳内;
●场强探头宜通过50Ω同轴电缆和示波器连接,并如图D.5 所示放置在屏蔽盒的边缘。
●同轴电缆的放置方式宜防止其接收辐射场(如同轴电缆和盒子十分接近,屏蔽电缆连接在盒 子上);
● 需要测量示波器上50Ω阻抗的电压降。静电放电宜通过接触的方式在屏蔽壳的大表面上 进行;
●宜移动静电放电发生器来测量和探头不同距离上的辐射场。
由测量到的探头负载的感应电压计算电场和磁场
●用数字示波器测量由静电放电发生器产生的辐射场造成的50Ω负载上的电压降v(t)。
● 计 算 v(t)的傅里叶变换V(w)。
●计算或测量使用的场探头的传递函数 T(w)。
● 依据V(w)/T(w) 的傅里叶反变换计算E(t) 和 H(t)。
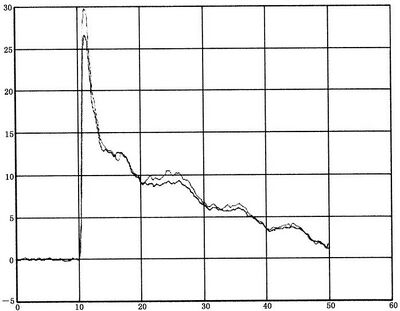
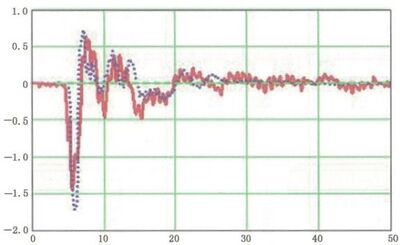
图 D.6 和 D.7 给出了一些结果。使用数值仿真数据是用来验证由环上测得电压降数据计算磁场的过程,反之亦然。
图 D.6 在距离环45 cm 处的电压降实测(实线)和数值仿真(点线)的比较(感应电压)
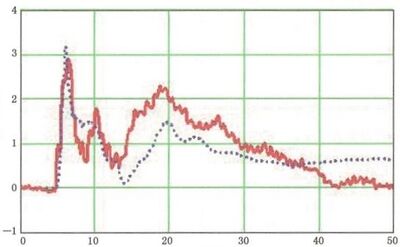
图 D.7 45 cm处测量结果计算出的磁场值(实线)和数值仿真计算(点线)的比较
D.6 用来估算由静电放电发生器产生的辐射场和感应电压的简单程序
以下的程序可以用通过测得的静电放电电流来估算静电放电发生器产生的辐射场:
●在尖端水平上使用标称值的或测得的静电放电电流。
●受扰电路被认为是短路的,并且第一步近似认为单位线参数可以被忽略。
一旦干扰场在时域上可知,感应电压可由图D.8 的等效电路来计算。
● 对于至少有一个低负载阻抗的回路(例如高速数字设备),电场分量可以忽略不计。
● 磁场可以由简单的等式计算:H=I/(2πr), 式 中r 是电流尖端到受扰回路的距离。其他的例 如静电放电继电器内电流,位移电流,接地带等可以忽略不计。
● 估算值(最糟糕情况)和实际从试验布置得到值之间的比较用来量化差异(例如图 D.9 的磁 场)。
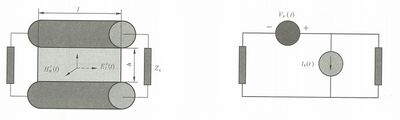
图 D.8 辐射场结构示意和等效电路图
说 明 :
r=45 cm 处的磁场辐射。
实线——测量值;
点线——由I/(2πr) 计算;
I是测得的静电放电电流。
图 D.9 磁场辐射
D.7 参考文件
参见参考文献[4]自由空间电厂传感器静电放电辐射场的数值预报和测量。
附 录 E
(资料性附录)
测量不确定度(MU) 的考虑
E.1 总 则
EMC 试验的重复性取决于影响试验结果的许多因素或影响量。这些影响量带来了误差,产生的骚 扰量可以分为随机效应或系统效应。本部分中定义的骚扰量值和实际骚扰量值的符合性通常由一系列 的测量确定(例如用带衰减器的示波器测量上升时间)。每个测量结果只是被测量的近似值,由于测量 不确定度的原因,测量值在一定程度上不同于真值。决定不确定度的关键因素是与试验仪器相关的校 准不确定度。
为了获得 一个高可 靠 性的校准结果,有必要识别测量设备中相关不确定度的来源,对测量不确定度 做出声明。
E.2 不确定度的分类
通常测量误差有两组分量:随机分量(参考下A 和系统分量(参考联下B 类)。随机性不确定 度和不可预知的影响相关联。系统性不确定度通常和测量仪器相关。系统分量有时能减少或修正,但 是根据定义随机分量不能诚少或修正。在 个给定的测量系统中存在很多可能影响这两个分量的 因 素 。
一个测武方法中的随机性不确定度可能会奋另一个使用手前者结果的测试方法中度成系统性不 确定度。为了避免这种可能的混乱,不确定度贡献的类型,不分为系统性和随机性的不确定度,而是分 为以下两类:
——A 类:用统计的方法评定,估算一系列的试验标准差。它们通常服从正态或高斯分布。
| 分布 | 合成不确定度 | 备注 |
|---|---|---|
| 正态或高斯 | [math]\displaystyle{ U_{\mathrm{C}}(y)=\sqrt{\frac{1}{(n-1)}\sum_{j=1}^{n}(u_{j}-\overline{u})^{2}} }[/math] | 通常来自验证记录 |
——B 类:由其他方法评定。它们通常与失 配 、电缆损耗以及仪器非线性特性相关。可以基于校准 数据,仪器制造商的规范或简单的通过知识和经验在分析中评估 B 类不确定度的大小和 分 布 。
对 A 类 和B 类进行分类并不意味这两部分有本质上的差异,只是基于其评估性质的区分。两种类 型都可以具有概率分布且任一类型所导致的不确定度分量均可用标准差量化。
E.3 局限
以下局限和条件用于本文中的考量:
● 不确定度报告局限于测量仪器造成的不确定度(B 类不确定度)。然而,这并不意味着试验室要 忽略 A 类不确定度的影响,而是宜由每个测试实验室独立评估,以此更全面地获得它们的测量不确定度。
● 假设所有的贡献量互不相关。
● 95%的置信度是可接受的。
注:表E.1, 表 E.2 和表E.3给出了B类不确定度报告的实例。
E.4 B 类不确定度的计算
标准不确定度是由给定值除以概率分布的除数来计算的。
此标准中每个概率分布的除数是:
| 分布 | 除数 | 备注 |
|---|---|---|
| 正态 | 包含因子k | 对于95%置信度k=2 通常来自校准证书 |
| 矩形 | √3 | 通常来自仪器制造商的数据 |
| U型 | √2 | 失配不确定度 不确定度贡献最可能在限制边界 |
在所有不确定度分布未知的情况下以矩形分布作为默认模式。
计算任何试验的合成标准不确定度都涉及合成单个标 准 不确定度,当所有数量单位相同,互不相 关,且在对数刻度下相加时合成是有效的。然硕静电放电校准和测量的单位需用百分数给出;计算公 式为:
[math]\displaystyle{ 10^{\frac{(unit_in_dB)}{20}}\times100 }[/math]
计算的结果是合成标准不 确定度:n( y )
[math]\displaystyle{ u_c(y)=\sqrt{\sum_{i=1}^mu_i^2(y)} }[/math]
u,(y) 定 义为单个 标准 不 确定 度。
假设输出变量v 服从正态分布,其不确定度的包含因子(即乘数)由学生t 分布给出。
u.(y) 通过乘以一个 包含因 子(k) 得到一个置信度更高的扩展不确定度U 。包含因子通过自由度 获得,根据A 类 和 B 类不 确定度之间的关系计算。
E.5 不确定度报告的编制
不确定度报告列出了测量中可能的误差来源及其概率分布的估计值。
不确定度报告的计算需以下步骤:
a) 说明骚扰量(例如由仪器产生的骚扰量)的特性;
b) 识别其不确定度的分量和值;
c) 确定各个分量的概率分布;
d) 计算各个分量的标准不确定度u(xi)
e) 计算合成标准不确定度 u(y), 包含因子k,和扩展不确定度U =u(y)×k;
f) 应用扩展不确定度;
g) 如有必要在质量文件中注明扩展不确定度(除非有要求,测试实验室不需要在报告中出具这些 数据)。
E.6 给出了确定的分量和关联值下不确定度报告的实例。需要注意的是,这些是用于指导的,而校 准或测试试验室宜注意,为自己特定的试验布置确定实际分量和值(例如最终报告可能确定了宜被考虑 在内的最少分量。测试试验室需要确定额外分量。这有利于提供试验室之间不确定度的比较。)
E.6 静电放电不确定度的影响量
静电放电校准和测试的不确定度不能用和发射或其他测量一样的方式来处理,因为静电放电试验 是没有数值结果的,仅仅给出一个简单的通过或失败的试验结果。静电放电试验期间,多个参数表征的 骚扰量特性施加于受试样品。监视或观察受试样品上一个或多个可观测信号,并和约定的判据进行比 较,以此来得到试验结果(通过/失败)。
注1:对于校准,受试样品等于被校准的静电放电发生器。
注2:本段中测量仪器是指校准用仪器。
原则上来说, 一个经典的测量不确定度可应用于受试样品上信号的测量。由于监测的测试过程是 针对特定的受试样品进行的,基础的标准不能够也不宜处理监测系统(观察者)的测量不确定度,虽然, 这是可以执行的。
也可以指定骚扰量参数的不确定度。由此,它们描述了指定仪器在基础标准规格内的符合程度。
这些为特定测量仪器得出的不确定度,不能用来描述基础标准定义的模拟电磁现象和实验室外部 世界真实的电磁现象之间的符合程度。因此,关于骚扰量定义的问题(例如静电放电枪对靶平面的位 置)和测量仪器的不确定度无关。
由于受试样品上的骚扰量参数的影响量是先验未知的,而且大部分情况下受试样品呈现出非线性 系统特性,单一不确定度数值不能用来定义骚扰量整体的不确定度。每个骚扰量参数都应有特定的不 确定度,这可能会使试验产生不止一个的不确定度报告。
注3:本附录的重点在于给出了校准不确定度的一个实例。
下面给出了评估测量仪器和试验布置的分量:
● 峰值读数;
● 10%峰值电流的时间读数;
● 90%峰值电流的时间读数;
● 30 ns 和60 ns 的时间读数;
● 低频转移阻抗 Zsys;
● 静电电压;
● 示波器失配链;
● 靶-衰减器-电缆链;
● 示波器水平测量分量;
● 示波器垂直测量分量;
● 测量系统的重复性(A 类);
● 静电放电发生器方向(A 类);
● 静电放电发生器定位(A 类);
● 试验布置的变化(A 类);
● 靶,示波器和衰减器的校准。
应认识到,校准和试验的分量可能是不同的。这导致每个过程(略微)不同的不确定度报告。
如静电放电枪的方向等方面可认为是A 类的不确定度,而且在本部分中一般不涉及到这些不确定 度。一个例外就是已经考虑的测量和校准测量系统的重复性。
E.7 校准结果的不确定度
建议对每个校准项生成独立的不确定度报告,即 Ip,I30,I60,tr。对于一次静电放电试验,骚扰量为 由静电放电发生器施加到受试样品上的放电电流。此骚扰量的校准项为Ip,I30,I60和tr。如 E.6 所述, 每个参数需单独计算不确定度报告。
表E.1、表 E.2 和表E.3 给出了这些参数计算好的不确定度报告实例。表中包括了对这些实例来说 认为对不确定度报告最重要的分量,每个分量的具体信息(数值、分布类型等)以及用来决定每个不确定 度报告的计算结果。
表 E.1 静电放电上升时间校准的不确定度报告实例
| 因素 | 分布 | 值 ps | ui(y) ps | ui(y)² ps² | 备注 |
|---|---|---|---|---|---|
| 峰值读数 | 正态k=2 | 50 | 25 | 625 | 峰值6.3%不确定度 (表E.2)乘以测得的上升时间800 ps |
| 90%峰值电流的时间读数 | 矩形因子=√3 | 25 | 14 | 196 | 示波器采样率20 GS/s |
| 10%峰值电流的时间读数 | 矩形因子=√3 | 25 | 14 | 196 | 示波器采样率20 GS/s |
| 总示波器水平测量因素(注1) | 正态k=2 | 36 | 18 | 324 | 来源于示波器的校准试验室 |
| 靶-衰减器-电缆链 | 正态k=2 | 30 | 15 | 225 | 来源于示波器的校准试验室(注2) |
| 重复性 | 正态因子=1 | 45 | 45 | 2025 | 由A类评估获得(注3) |
| 总计 | 3591 | ||||
| 上升时间的合成标准不确定度ue | 根 | 60 ps | |||
| 上升时间的扩展不确定度U | 正态k=2 | 120 ps (15%) | 置信度95% | ||
| 注1: 总示波器水平测量值因素包括示波器水平分辨率,插值分辨率,时基分辨率,频率测量,上升时间修正等不确定度因素。 注2: 链的校准证书通常只包括衰减的频率响应。在此假设,上升时间测量的不确定度分量也由校准试验室提供,因此k=2。 注3: 重复性需要至少5次的连续测量。这是A类评估,由n次重复测量得到标准差s(可)的公式为: [math]\displaystyle{ s\left(\overline{q}\right)=\sqrt{\frac{1}{n\left(n-1\right)}\sum_{j=1}^{n}\left(q_{j}-\overline{q}\right)^{2}} }[/math] 其中qj:第j次的测量结果;[math]\displaystyle{ \overline{q} }[/math]:结果的算术平均值。 | |||||
表 E.2 静电放电峰值电流校准的不确定度报告实例
| 分量 | 分布 | 值 % | ui(y) % | ui(y)² %² | 备注 |
|---|---|---|---|---|---|
| 总示波器垂直测量 分量(注1) | 正态k=2 | 3.2 | 1.6 | 2.56 | 来自校准实验室 |
| 靶-衰减器-电缆链 | 正态k=2 | 3.6 | 1.8 | 3.24 | 来自校准实验室 |
| 示波器链的不匹配 | U形 因子= √ 2 | 2 | 1.4 | 2 | 来自校准或技术规范(注2) |
| 低频转移阻抗 | 正态k=2 | 6×10-6 | 3×10-6 | 9×10-12 | 内部校准(注3) |
| 重复性 | 因子=1 | 1.5 | 1.5 | 2.25 | 由A类评估获得(注4) |
| 总计 | 10.05 | ||||
| 峰值电流的合成标 准不确定度uc | 根 | 3.17 | |||
| 峰值电流的扩展不 确定度 | k=2 | 6.3% | 置信度95% | ||
| 注 1:总示波器垂直测量分量包括示波器垂直分辨率、低频线性度、高频线性度、偏置分辨率等。校准需要覆盖全频段,即 f ≤ 2 GHz。然而,在截止频率为 fc = 2 GHz 的一阶滤波器下,平坦度不必更好,即 [math]\displaystyle{ A(f)\sim\mid1+(f/f_{\mathrm{c}})^2\mid^{-1/2} }[/math]。 注 2:失配分量是由轭-衰减器-电缆链的输出反射系数 Γc 和示波器的输入反射系数 Γ0 来决定的。他们宜从校准证书或技术规范上获得。由于 Γ 中二阶分量的误差,一个可靠的技术规范就够了。但是请注意,技术规范也要覆盖全频段,示波器通常不是这样,所以需要额外的测量。 失配分量:Γc× Γ0,U 型分布,因此除数为 √2。 这个失配不确定度的公式假设了示波器的幅度响应已根据射频校准的概念进行了校准,即电压误差是基于 50Ω 源的人射电压而不是输入的实际电压。这宜在证书上核实,否则需应用不同的公式。 注 3:这里假定试验室有一个单独的校准指导书,其不确定度的评估得到此校准的扩展不确定度 U。 注 4:至少取得连续 5 次的测量值来得到重复性。这是 A 类评估,由 n 次重复测量值得到标准差 [math]\displaystyle{ s\left(\overline{q}\right) }[/math]的公式为: [math]\displaystyle{ s(\overline{q})=\sqrt{\frac{1}{n(n-1)}\sum_{j=1}^{n}(q_{j}-\overline{q})^{2}} }[/math] 其中 qj,第 j 次的测量结果;[math]\displaystyle{ \overline{q} }[/math],结果的算术平均值。 | |||||
表 E.3 静电放电中I ₃0,I 6o校准不确定度评估实例
| 分量 | 分布 | 值 % | ui(y) % | ui(y)² %² | 备注 |
|---|---|---|---|---|---|
| 表E.2的不确定度 | 正态k=2 | 6.3 | 3.15 | 9.92 | 峰值电流的不确定度(表E.2) |
| 30 ns或60 ns的时间读数 | 矩形 k=√3 | 0.17 | 0.098 | 0.0096 | 对于10%峰值电流到30 ns或60 ns之间的时间间隔的测量,30 ns或60 ns时电流读数的灵敏度。20 GS/s采样率的示波器(两个读数各自具有50 ps的不确定度) |
表 E.3 (续)
| 分量 | 分布 | 值 % | ui(y) % | ui(y)2 %2 | 备注 |
|---|---|---|---|---|---|
| 总计 | 9.93 | ||||
| U. | 根 | 3.15% | |||
| I₃₀和I₆₀的扩展不确定度U | 正态 k=2 | 6.3% | 置信度95% |
产品委员会或认证机构可提供其他解释。
E.8 静电放电发生器符合规范的不确定度应用
一般来说,为了确保发生器在其规范内,校准结果应在本部分规定的限值内容差不减去测量不确 定度)。
下列推荐的用于进行校准的试验室使用的测量不确定度:
上升时间 tr M U≤15 %
峰值电流Ip MU ≤7%
30 ns 时的电流 MU ≤ 7
60 ns 时的电流 MU ≤7
附 录 F
(资料性附录)
试验结果的变化和调整策略
F.1 试验结果的变化
由于静电放电本身的复杂性和试验设备固有的偏差,可预料到静电放电试验的结果会有一些变化。 通常,这些变化表现为在不同的测试等级出现错误或者试验过程中受试设备出现不同类型的错误。根 据它们出现错误的试验等级,这些试验结果变化可以影响对受试设备是否通过试验的决定。
在试验结果有差异的情况下,通常用以下步骤来判定差异的来源。
● 验证试验布置;检查所有细节,包括每一根电缆的摆放和受试设备的条件(例如盖子、门)。
● 验证试验程序,包括受试样品的操作模式,辅助设备的摆放和位置,操作者的位置,软件状态, 对受试设备放电的施加。
● 验证试验发生器;是否运行正常?最后校准日期?是否在规范内运行?试验结果的不同是因 为使用了不同的发生器吗?
如果试验结果的差异是因为使用了不同的静电放电发生器,满足6.2要求的任何发生器作出的结 果都可以用来确定与本部分的符合性。
F.2 调整策略
当所有试验条件,包括静电放电发生器都相同的情况下,如果出现试验结果的差异,则以下调整策 略可用于确定本部分的符合性。该策略将被单独应用到每一个出现试验结果变化的试验点。
a) 第一次试验是根据8.3在预期的试验等级下,对试验点进行规定数量的放电(例如放电50次)。 如果在此第一组放电下没有出现不可接受的影响,则受试设备在该试验点上通过试验。如果 在这组放电下出现了一次不可接受的影响,要根据下述 b) 进行进一步试验。如果在这组放电 下出现超过一次不可接受的影响,受试设备在该试验点上就没有通过试验。
b) 第二次试验是在预期的试验等级下,对试验点上施加新一组加倍次数的放电。如果在这组放 电下没有出现不可接受的影响,受试样品在该试验点上和试验等级下通过了试验。如果在这 组放电下出现了一次不可接受的影响,可根据下述c) 进行进一步试验;否则受试设备在该试 验点上的试验不通过。如果在这组放电下出现超过一次的不可接受的影响,受试设备在该试 验点上的试验不通过。
c) 第三次试验是在预期的试验等级下,对试验点施加新一组和 b) 一样数量的放电。如果在这组 放电下没有出现不可接受的影响,受试设备在该试验点上通过了试验。如果在这组放电下出 现一个或多个不可接受的影响,受试设备在该试验点上的试验不通过。
参 考 文 献
[1] IEC 60050-311 International electrotechnical vocabulary—Part 311:General terms relating to electrical measurement
[2] IEC 61000-6-1 Electromagnetic compatibility(EMC)-Part 6-1:Generic standards—Im- munity for residential,commercial and light-industrial environments
[3] IEC Guide 107 Electromagnetic compatibility—Guide to the drafting of electromagnetic compatibility publications
[4] S.Caniggia,F.Maradei,Numerical Prediction and Measurement of ESD Radiated Fields by Free-Space Field Sensors,IEEE Trans.on EMC,Vol.49,August 2007